Hamiltonian Graphs

HAMILTONIAN GRAPHS: Hamiltonian graphs are named after Sir William Hamilton, an Irish mathematician who introduced the problems of finding a circuit in which all vertices of a graph appear exactly once.

1. A circuit in a graph G that contains each vertex in G exactly once, except for the starting and ending vertex that appears twice is known as Hamiltonian circuit.
2. A graph G is called a Hamiltonian graph, if it contains a Hamiltonian circuit.
3. A Hamiltonian path is a simple path that contains all vertices of G where the end points may be distinct.

Note that an Eulerian circuit traverses every edge exactly once, but may repeat vertices, while a Hamiltonian circuit visists each vertex exactly once but may repeat edges. While there is a criterion for determining whether or not a graph contains an Eulerian circuit, a similar criterion does not exist for Hamiltonian ciruits.

In the following figures, hamiltonian path and cycles are shown :

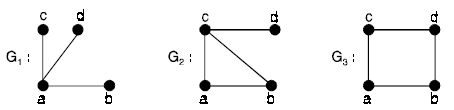
The graph G1 has no hamiltonian path (and so hamiltonian cycle), G2 has hamiltonian path abcd but no hamiltonian cycle, while G3 has hamiltonian cycle abdca.

The cycle Cn with n distinct (and n edges) is hamiltonian. Moreover given hamiltonian graph G then if G′ is a subgraph obtained by adding in new edges between vertices of G, G′ will also be hamiltonian. Since any hamiltonian cycle in G will also be hamiltonian cycle in G′. In particular kn, the complete graph on n vertices, in such a supergraph of a cycle, kn is hamiltonian.

A simple graph G is called maximal non-hamiltonian if it is not hamiltonian but the addition to it any edge connecting two non-adjacent vertices forms a hamiltonian graph. The graph G2 is a maximal non-hamiltonian since the addition of an edge bd gives hamiltonian graph G3.