Hand Shaking Dilemma And Directed Walk Path And Circuit

HAND SHAKING DILEMMA: In a digraph D, the sum of the out-degree of all vertices is equal to the sum of the in-degrees of all vertices, each sum being equal to the numbe of edges in D.
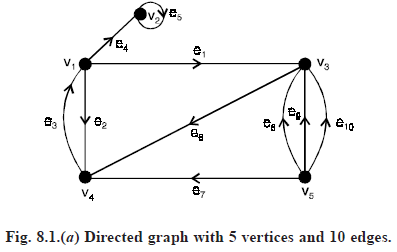
For example, the digraph in Fig. 8.1, we note that the digraphs has 6 vertices and 9 edges and that the sums of the out-degrees and in-degrees of its vertices are

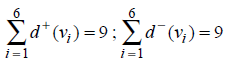
DIRECTED WALK, DIRECTED PATH, DIRECTED CIRCUIT

Directed walk: A directed walk or a directed trail in D is a finite sequence whose terms are alternately vertices and edges in D such that each edge is incident out of the vertex preceeding it in the sequence and incident into the vertex following it.

A directed walk or a directed trail in D is a sequence of the form v0 e1 v1 e2 ..... ek vk where v0, v1, ...... vk are vertices of D in some order and e1, e2, ..... ek are edges of D such that the edge ei has vi – 1 as the initial vertex and vi as the terminal vertex, i = 1, 2, ..... k.

A vertex can appear more than once in a directed walk but not an edge.

The vertex with which a directed walk begins is called its initial vertex and the vertex with which its ends is called its final or terminal vertex.

Directed path
An open directed walk in which no vertex is repeated is called a directed path.

Directed circuit
A closed directed walk in which no vertices, except the initial and final vertices are repeated is called a directed circuit or a directed cycle.

Length
The number of edges present in a directed walk, directed path, directed circuit is called its length.

For example, in the digraph shown in Fig. (8.1)
(i) v1e1v2e2v3e3v3 is an open directed walk which is not a directed path, its length is 3.
(ii) v6e6v1e1v2e2v3 is an open directed walk which is a directed path, its length is 3.
(iii) v1e1v2e9v1 or v1v2v1 is a closed directed walk which is a directed circuit, its length is 2.