Heuristic Algorithm For An Upper Bound
Heuristic algorithm for an upper bound on the travelling salesmen problem
1) Start with a finite set of 3 or more vertices, each pair joined by a weighted edge.
2) Choose any vertex and find a vertex joined to it by an edge of least weight.
3) Find the vertex which is joined to either of the two vertices identified in step (2) by an edge of least weight. Draw these three vertices and the three edges joining them to form a cycle.
4) Find a vertex, not currently drawn, joined by an edge of least weight to any of the vertices already drawn. Label the new vertex vn and the existing vertex to which it is joined by the edge of least weight as vk. Label the two vertices which are joined to vk in the existing cycle as vk-1 and vk 1. Denote the weight of an edge vpvq by w(vpvq). If w(vnvk-1) – w(vkvk-1) < w(vnvk 1) – w(vkvk 1) then replace the edge vkvk-1 in the existing cycle with the edge vnvk-1 otherwise replace the edge vkvk 1 in the existing cycle with the edge vnvk 1. See sketch below.
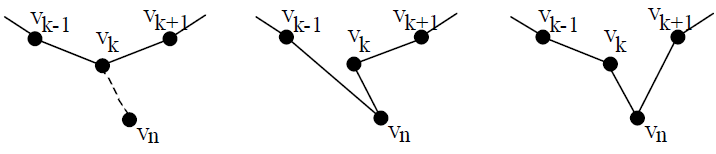
5) Repeat step 4 until all vertices are joined by a cycle, then stop. The cycle of obtained is an upper bound for the solution to the travelling salesmen problem.
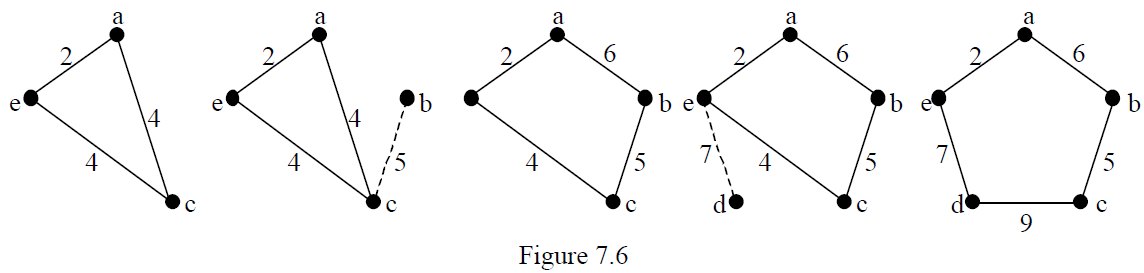
Applying this to our previous problem we proceed thus. Start by choosing vertex a, then the edge of least weight incident to a is ae and the vertex adjacent to {a,e} joined by an edge of least weight is c. Form the cycle aeca. Now the vertex adjacent to {a,c,e} joined by an edge of least weight is b (edge bc) and the vertices adjacent to c in the existing cycle are a and e. In this case w(be) – w(ce) = w(ba) – w(ca) so we can create the new cycle by replacing either of edges ca or ce. We will choose ca. Now the vertex adjacent to {a,b,c,e} joined by an edge of least weight is d (edge ed) and the vertices adjacent to e in the existing cycle are a and c. Now w(da) – w(ea) > w(dc) – w(ec) so we create the new cycle by replacing edge ec with edge dc. The cycle is abcdea and the weight is 29.
What would have happened if we’d chosen a different starting vertex? Let’s try it. Start by choosing vertex b, then the edge of least weight incident to b is bc and the vertex adjacent to {b,c} joined by an edge of least weight is a or e. Choose a and form the cycle abca. Now the vertex adjacent to {a,b,c} joined by an edge of least weight is e (edge ae) and the vertices adjacent to a in the existing cycle are b and c. In this case w(eb) – w(ab) < w(ec) – w(ac) so we can create the new cycle by replacing edge ab with eb, creating the cycle aebca. Now the vertex adjacent to {a,b,c,e} joined by an edge of least weight is d (edge de) and the vertices adjacent to e in the existing cycle are a and b. Now w(da) – w(ea) > w(db) – w(eb) so we create the new cycle by replacing edge eb with edge db. The cycle is acbdea and the weight is 26.
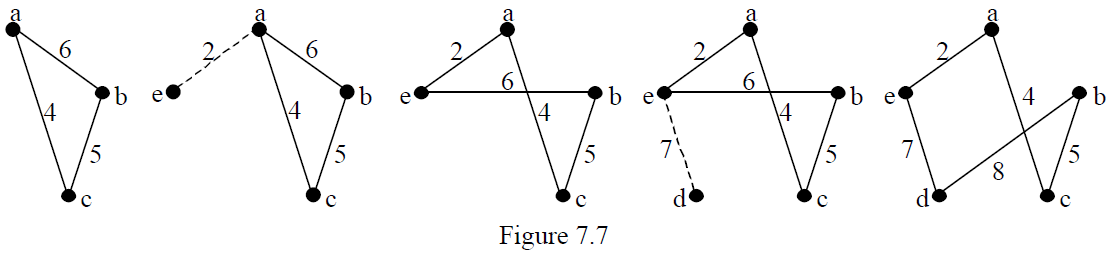
So different starting points and different choices will give different upper bounds! It is a heuristic algorithm and there is no theory to tell us how to make choices which result in a least upper bound, trial and error is the only way forward!