Huffman Code

Huffman coding: We now introduce an algorithm that takes as input the frequencies (which are the probabilities of occurrences) of symbols in a string and produces as output a prefix code that encodes the string using the fewest possible bits, among all possible binary prefix codes for these symbols. This algorithm, known as Huffman coding.

Note that this algorithm assumes that we already know how many times each symbol occurs in the string so that we can compute the frequency of each symbol of dividing the number of times this symbol occurs by the length of the string.

Huffman coding is a fundamental aglorithm in data compression the subject devoted to reducing the number of bits required to represent information.

Huffman coding is extensively used to compress bit strings representing text and it also plays an important role in compressing audio and image files.

Algorithm : Huffman coding: Procedure Huffman (C : symbols ai with frequencies Wi, i = 1, ......, n)
F : = forest of n rooted trees, each consisting of the single vertex ai and assigned weight Wi.
While F is not a tree
begin
Replace the rooted trees T and T′ of least weights from F with W(T) ≥ W(T′) with a tree having a new root that has T as its left subtree and T′ as its right subtree. Label the new edge to T with 0 and the new edge to T′ with 1.
Assign W(T) W(T′) as the weight of the new tree.
end
{the Huffman coding for the symbol ai is the concatenation of the labels of the edges in the unique path from the root to the vertex ai}

Given symbols and their frequencies, out goal is to construct a rooted binary tree where the symbols are the labels of the leaves. The algorithm begins with a forest of trees each consisting of one vertex, where each vertex has a symbol as its label and where the weight of this vertex equals the frequency of the symbol that is its label. At each step we combine two trees having the least total weight into a single tree by introducing a new root and placing the tree with larger weight as its left subtree and the tree with smaller weight as its right subtree.

Furthermore, we assign the sum of the weights of the two subtrees of this tree as the total weight of the tree. The algorithm is finished when it has constructed a tree, that is, when the forest is reduced to a single tree.

Note that Huffman coding is a greedy algorithm. Replacing the two subtrees with the smallest weight at each step leads to an optimal code in the sense that no binary prefix code for these symbols can encode these symbols using fewer bits.

There are many variations of Huffman coding
For example, instead of encoding single symbols, we can encode blocks of symbols of a specified length, such as blocks of two symbols. Doing so many reduce the number of bits required to encode the string. We can also use more than two symbols to encode the original symbols in the string. Furthermore, a variation known as adaptive Huffman coding can be used when the frequency of each symbol in a string is not known in advance, so that encoding is done at the same time the string is being read.
In other words, a prefix code where in the shorter sequences are used for the more frequently occurring symbols. If there are many symbols, such as all 26 letters of the alphabet, a trial-and-error methods for constructing such a tree is not specified. An elegant construction developed by Huffman provides a technique for constructing such trees. The general problem of constructing an efficient tree can be described as follows :

Let w1, w2, ...... wn be a set of positive numbers called weights, where w1 ≤ w2 ≤ ...... ≤ wn. If T = (V, E) is a complete binary tree with n leaves, assign these weights to the n leaves. The result is called a complete binary tree for the weights w1, w2, ......, wn.
The weight of the tree, denoted W(T), is defined as , where for each 1 ≤ i ≤ n, l(wi) is the level number of the leaf assigned the weight wi. The objective is to assign the weights so that W(T) is as small as possible.
A complete binary tree T′ for these weights is said to be an optimal tree if W(T′) ≤ W(T) for any other complete binary tree T for the weights.

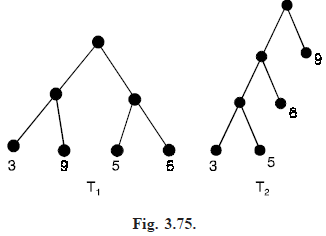
Fig. (3.75) shows two complete binary trees for the weights 3, 5, 6 and 9. For tree T1, W(T1) = 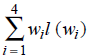= (3 9 5 6) . 2 = 46 because each leaf has level number 2. In the case of T2, W(T2) = 3.3 5.3 6.2 9.1 = 45, which is optimal.

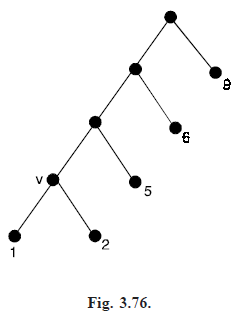
Huffman construction is that in order to obtain an optimal tree T for the n weights w1, w2, w3, ......, wn, one considers an optimal tree T′ for the n – 1 weights w1 w2, w3, ......, wn. In particular, the tree T′ is transformed into T by replacing the leaf v having weight w1 w2 by a tree rooted at v of height 1 with left child of weight w1 and right child of weight w2. If the tree T2 in Fig. (3.75) is optimal for the four weights 1 2, 5, 6, 9, then the tree in Fig. (3.76) will be optimal for the five weights 1, 2, 5, 6, 9.