Infix, Prefix And Postfix Notation Of An Arithmatic Operation

INFIX, PREFIX AND POSTFIX NOTATION OF AN ARITHMETIC EXPRESSION
We know that even for fully parenthesised expression a repeated scanning of the expression is still required in order to evaluate the expression. This phenomenon is due to the fact that operators appear with the operands inside the expression. We can represent expressions in three different ways. They are Infix, Prefix and Postfix forms of an expression.

Infix notation: The notation used in writing the operator between its operands is called infix notation. The infix form of an algebraic expression is the inorder traversal of the binary tree representing the expression. It gives the original expression with the elements and operations in the same order as they originally occured. To make the infix forms of an expression unambiguous it is necessary to include parentheses in the inorder traversal whenever we encounter an operation.

Prefix notation
The repeated scanning of an infix expression is avoided if it is converted first to an equivalent parenthesis free of polish notaiton. The prefix form of an expression is the preorder traversal of the binary tree representing the given expression. The expression in prefix notation are unambiguous, so that no parentheses are needed in such expression.

Postfix notation
The postfix form of an expression is the postorder traversal of the binary tree representing the given expression. Expressions written in postfix form are said to be in reverse polish notation. Expressions in this notation are unambiguous, so that parentheses are not needed. Table below gives the equivalent forms of several fully parenthesised expressions. Note that in both the prefix and postfix equivalents of such an infix expression, the variable names are all in the same relative position.

Evaluating prefix and postfix form of an expression
To evaluate an expression in prefix form, proceed as follow move from left to right until we find a string of the form Fxy, where F is the symbol for a binary operator and x and y are two operands. Evaluate xFy and substitute the result for the string Fxy. Consider the result as a new operand and continue this procedure until only one number remains. When an expression is in postfix form, it is evaluated in a manner similar to that used for prefix form, except that the operator symbol is after its operands rather than before them.

Problem. Represent the expression as a binary tree and write the prefix and postfix forms of the expression
A * B – C ↑ D E/F
Solution. The binary tree representing the given expression is shown below.

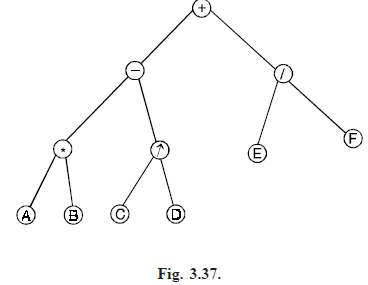
Prefix : – * AB ↑ CD/EF
Postfix : AB * CD ↑ – EF/

Problem. What is the value of
(a) Prefix expression x – 84 6/42
(b) Postfix expression 823 * 2 ↑ 63/

Solution. (a) The evaluation is carried out in the following sequence of steps
(i) x – 84 6/42
(ii) x4 6/42 since the first string in the Fxy is – 84 and 8 – 4 = 4.
(iii) x4 62 replacing /42 by 4/2 = 2
(iv) x48 replacing 62 = 8
(v) 32 replacing x48 by 4x8 = 32
(b) The evaluation is carried out in the following sequence of steps.
(i) 823 * – 2 ↑ 63/
(ii) 86 – 2 ↑ 63/ replacing 23* by 2 * 3 = 6
(iii) 22 ↑ 63/ replacing 86 – by 8 – 6 = 2
(iv) 463/ replacing 2 ↑ 2 by 22 = 4
(v) 42 replacing 63/by 6/3 = 2
(vi) 6 replacing 42 by 4 2 = 6.