Introduction To Graph Coloring

Introduction

• When a map is colored, two regions with a common border are customarily assigned different colors.
• We want to use a small amount of colors instead of just assigning every region its own color.
• Each map in a plane can be represented by a graph.

1. Each region is represented by a vertex.
2. Edges connect to vertices if the regions represented by these vertices have a common border.
3. Two regions that touch at only one point are not considered adjacent.

• The resulting graph is called the dual graph of the map.
• A coloring of a simple graph is the assignment of a color to each vertex of the graph so that no two adjacent vertices are assigned the same color.
• The chromatic number of a graph is the least number of colors needed for a coloring of the graph.
• The Four Color Theorem: The chromatic number of a planar graph is no greater than four.

Example: Chromatic number of the graph shown below

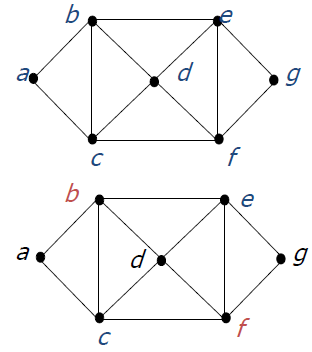
The chromatic number must be at least 3 since a, b, and c must be assigned different colors. So lets try 3 colors first.

3 colors work, so the chromatic number of this graph is 3.