Introduction To Tree

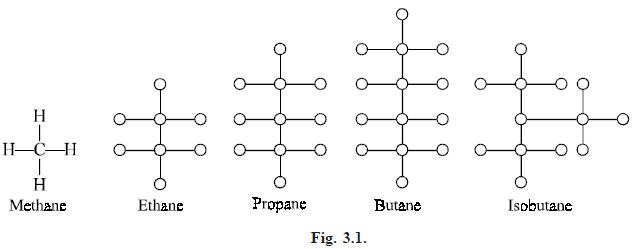
INTRODUCTION: A tree is a connected acyclic graph. Kirchhoff developed the theory of trees in 1847, in order to solve the system of simultaneous linear equations which give the current in each branch and arround each circuit of an electric network. In 1857, Cayley discovered the important class of graphs called trees by considering the changes of variables in the differential calculus. Later, he was engaged in enumerating the isomers of saturated hydro carbons Cn H2n 2 with a given number of n of carbon atoms as

Tree

1. Acyclic graph: A graph is acyclic if it has no cycles.
2. Tree: A tree is a connected acyclic graph.
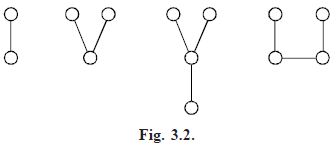
3. Forest: Any graph without cycles is a forest, thus the components of a forest are trees. The tree with 2 points, 3 points and 4-points are shown below :

Note :
(1) Every edge of a tree is a bridge. i.e., every block of G is acyclic. Conversely, every edge of a connected graph G is a bridge, then G is a tree.
(2) Every vertex of G (tree) which is not an end vertex is neccessarily a cut-vertex.
(3) Every nontrivial tree G has at least two end vertices.