Kruskal’s Algorithm

Kruskal’s algorithm: Start with a finite set of vertices, each pair joined by a weighted edge.
1 (List all the weights in ascending order)
2 (Draw the vertices and weighted edge corresponding to the first weight in the list provided that, in so doing, no cycle is formed. Delete the weight from the list)
3) Repeat step 2 until all vertices are connected, then stop. The weighted graph obtained is a minimum connector, and the sum of weights on its edges is the total weight of the minimum connector.

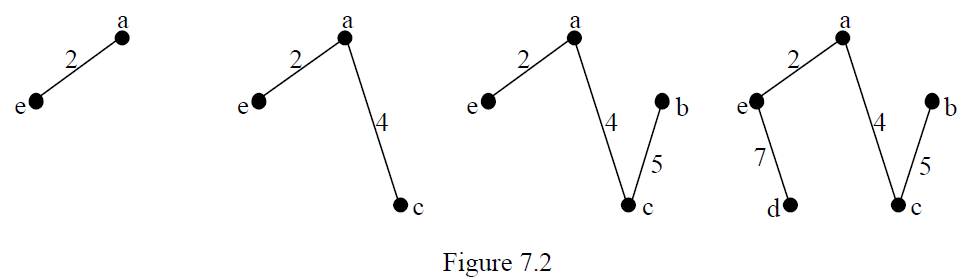
To construct a minimum spanning tree for the graph of figure 7.1 we proceed thus. The weights are

so the steps of Kruskal’s algorithm will give the following :- choose ae, choose ac, reject ce (would form cycle acea), choose bc, reject ab (would form cycle acba), reject be (would form cycle acbea), choose de. All vertices now connected. The total weight is 18

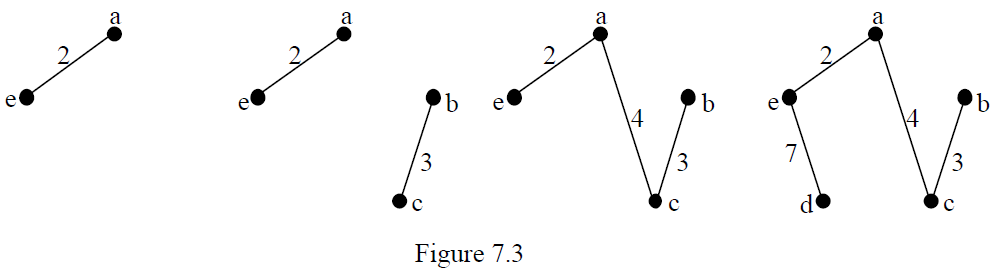
Although, in the above example, the subgraph constructed was a connected subgr aph at each stage this isn’t necessarily the case. For instance suppose edge bc had weigh 3 instead of 5. Now the weights are

so the steps of Kruskal’s algorithm will give the following :- choose ae, choose bc, choose ac, reject ce (would form cycle), reject ab (would form cycle), reject be (would form cycle), choose de. All vertices now connected. The total weight is 16.