Lines And Points In Graphs

CRITICAL POINTS AND CRITICAL LINES: If H is a subgraph of G, then α0 (H) ≤ α0 (G). In particular this inequality holds when H = G – v or H = G – x for any point v or line x.

If α0 (G – v) < α0 (G) then v is called a critical point, if α0 (G – x) < α0 (G) then x is a critical line of G. If v and x are critical, it follows that
α0 (G – v) = α0 (G – x) = α0 – 1.

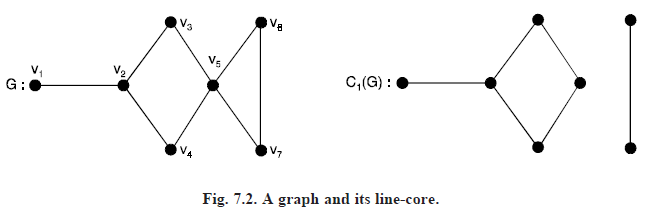
LINE-CORE AND POINT-CORE: The line-core C1 (G) of a graph G is the subgraph of G induced by the union of all independent sets Y of lines (if any) such that |Y| = α0 (G).

For example. Consider an odd cycle CP. Here we find that α0 (C_P) = (P 1)/2 but that β1 (C_P) = (P – 1)/2 so C_P has no line-core.

A minimum point cover M for a graph G with point set V is said to be external if for each subset M′ of M, |M′| ≤ |U (M′)|, where U (M′) is the set of all points of V – W which are adjacent to a point of M′.

Observations
(i) A covering exists for a graph if and only if the graph has no isolated vertex.
(ii) A covering of an n-vertex graph will have at least [n/2] adges. ([x] denotes the smallest integer not less than x)
(iii) Every pendent edge in a graph is include in every covering of the graph.
(iv) Every covering contains a minimal covering.
(v) If we denote the remaining edges of a graph by (G – g), the set of edges g is a covering if and only if, for every vertex v, the degree of vertex in (G – g) ≤ (degree of vertex v in G) – 1.
(vi) No minimal covering can contain a circuit, for we can always remove an edge from a circuit without leaving any of the vertices in the circuit uncovered. Therefore, a minimal covering of an n-vertex graph can contain no more than n – 1 edges.
(vi) A graph, in general, has many minimal coverings, and they may be of different sizes (i.e,. consisting of different numbers of edges). The number of edges in a minimal covering of the smallest size is called the covering number of the graph.