Matrices Over Gf(2) And Vector Spaces Of Graphs

Matrices over GF(2) and Vector Spaces of Graphs: The set {0, 1} is called a field (i.e. it follows the same arithmetic rules as real numbers) if addition and multiplication are defined as follows:

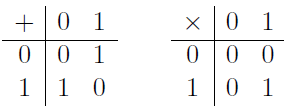
In this case −1 = 1 and 1−1 = 1. This is the field GF(2).
If we think of the elements 0 and 1 of the all-vertex incidence, cut, fundamental cut, circuit and fundamental circuit matrices of a (”undirected”) graph as elements of the field GF(2),

For ”undirected” graphs, the vector spaces are over the field GF(2). For directed graphs, the vector spaces are real (i.e. over the field R). The row space of the cut matrix of a (di)graph is the cut space. Similarly, the row space of the circuit matrix is the circuit space. The dimension of the cut space is the rank of the (di)graph and the dimension of the circuit space is the nullity of the (di)graph. Furthermore, the cut space and the circuit space are orthogonal complements. (All of these statements follow directly from the results above.)

Often, we deal with the above mentioned spaces through subgraphs, i.e. we identify a vector with the subgraph generated by the corresponding arcs. In the case of ”undirected” graphs, the addition of GF(2) vectors corresponds to the ring sum operation.