Matrix Representation Of Graphs
Matrix Representation of Graphs: The adjacency matrix of the graph G = (V,E) is an n × n matrix D = (dij), where n is the number of vertices in G, V = {v1, . . . , vn} and dij = number of edges between vi and vj . In particular, dij = 0 if (vi, vj) is not an edge in G. The matrix D is symmetric, i.e. DT = D.
Example.
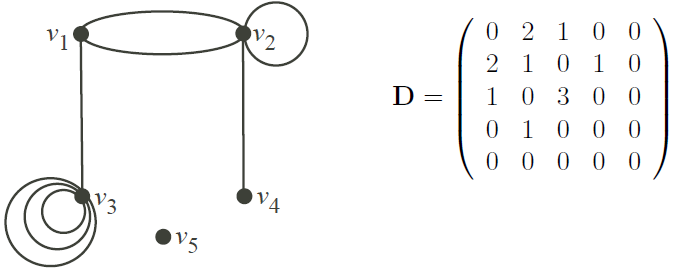
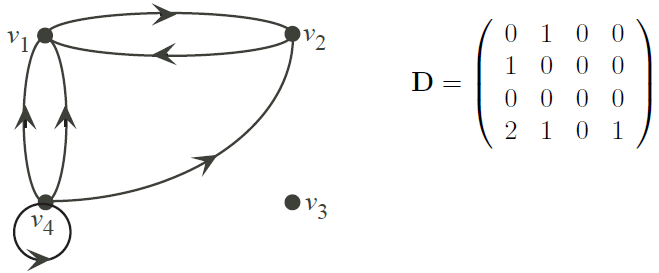
Obviously, an adjacency matrix defines a graph completely up to an isomorphism. The adjacency matrix of a directed graph G is D = (dij), where dij = number of arcs that come out of vertex vi and go into vertex vj .
The all-vertex incidence matrix of a non-empty and loopless graph G = (V,E) is an n×m matrix A = (aij), where n is the number of vertices in G, m is the number of edges in G and

Example.
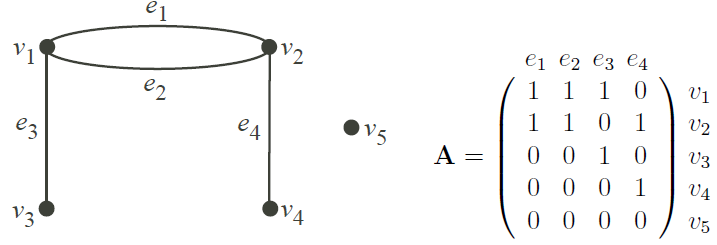
The all-vertex incidence matrix of a non-empty and loopless directed graph G is A = (aij), where

Example.
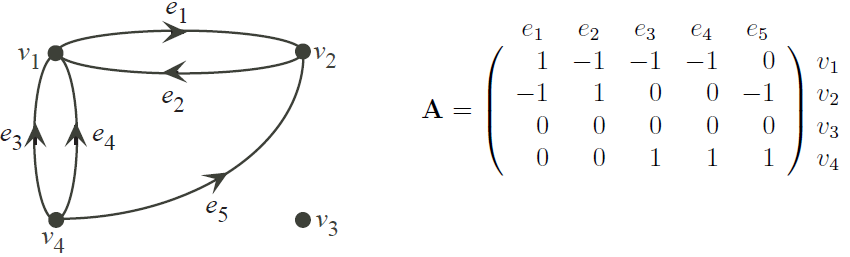
Since every column of an all-vertex incidence matrix contains exactly two non-zero numbers, two ones, we can remove a row and still have enough information to define the graph. The incidence matrix of a graph is obtained by removing a row from the all-vertex incidence matrix. It is not unique because there are n possible rows to remove. The vertex corresponding to the row removed is called the reference vertex.
Similarly, every column in the all-vertex incidence matrix of a digraph contains exactly two non-zero numbers, 1 and −1. We can remove a row from the all-vertex incidence matrix and obtain the incidence matrix. Notice that the rows of an all-vertex incidence matrix are linearly dependent because the sum of rows is a zero vector.