More Application Of Graph
MORE APPLICATIONS: In this section we consider, graph theory applications, taken from operational research, organic chemistry, electrical network theory and computing and each involving the use of trees.
The minimum connector problem: Let us suppose that we wish to build a railway network connecting n given cities so that a passenger can travel from any city to any other. If, for economic reasons, the total amount of track must be a minimum, then the graph formed by taking the n cities as vertices and the connecting rails as edges must be a tree.
The problem is to find an efficient algorithm for deciding which of the nn – 2 possible trees connecting these cities uses the least amount of track, assuming that the distances between all the pairs of cities are known.
As before, we can reformulate the problem in terms of weighted graphs. We denote the weight of the edge e by W(e), and our aim is to find the spanning tree T with least possible total weight W(T). Unlike some of the problems we considered earlier, there is a simple algorithm that provides the solution. It is known as a greedy algorithm, and involves choosing edges of minimum weight in such a way that nocycle is created.
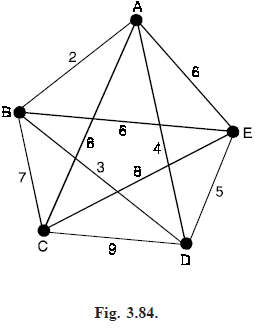
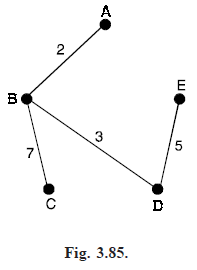
For example, if there are five cities, as shown in Fig. (3.84), then we start by choosing the edges AB (weight 2) and BD (weight 3). We cannot then choose the edge AD (weight 4), since it would create the cycle ABD, so we choose the edge DE (weight 5). We cannot then choose the edges AE or BE (weight 6), since each would create a cycle, so we choose the edge BC (weight 7). This completes the tree (see Fig. 3.85).
Enumeration of chemical molecules
One of the earliest uses of trees was in the enumeration of chemical molecules. If we have a molecule consisting only of carbon atoms and hydrogen atoms, then we can represent it as a graph in which each carbon atom appears as a vertex of degree 4, and each hydrogen atom appears as a vertex of degree 1.
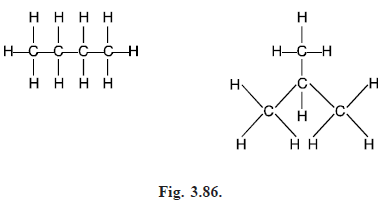
The graphs of n-butane and 2-methyl propane are shown in Fig. (3.86). Although they have the same chemical formula C4H10, they are different molecules because the atoms are arranged differently with in the molecules. These two molecules form part of a general class of molecules known as the alkanes or paraffins, with chemical formula CnH2n 2, and it is natural to ask how many different molecules there are with this formula.
To answer this, we note first that the graph of any molecule with formula Cn H2n 2 is a tree. Since it is connected and has n (2n 2) = 3n 2 vertices and {4n (2n 2)}/2 = 3n 1 edges.
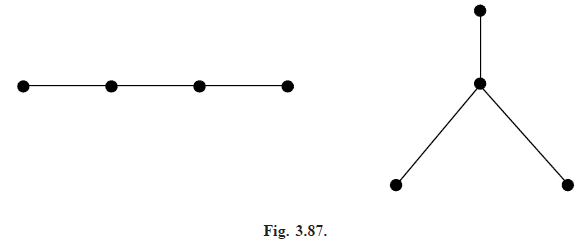
Note that the molecule is determined completely once we know how the carbon atoms are arranged, since hydrogen atoms can then be added in such a way as to bring the degree of each carbon vertex to 4. We can thus discard the hydrogen atoms, as in Fig. (3.87), and the problem reduces to that of finding the number of trees with n vertices, each of degree 4 or less.
Electrical neworks: Suppose that we are given the electrical network in Fig. (3.88), and that we wish to find the current in each wire.
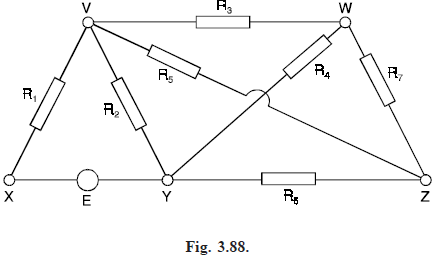
To do this, we assign an arbitrary direction to the current in each wire, as in Fig. (3.89), and apply Kirchhoff’s laws :
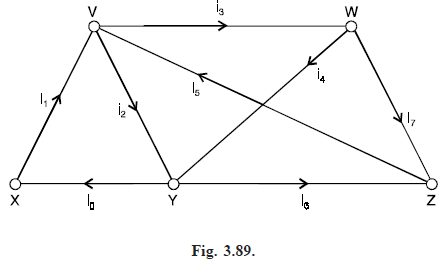
(i) the algebraic sum of the currents at each vertex is 0,
(ii) the toal voltage in each cycle is obtained by adding the products of the currents ik and resistances Rk in that cycle.
Applying Kirchhoff’s second law to the cycles VYXV, VWYV and VWYXV, we obtain the
equations. i1R1 i2R2 = E, i3R3 i4R4 – i2R2 = 0, i1R1 i3R3 i4R4 = E.
The last of these three equations is simply the sum of the first two, and gives us no further
information. Similarly, if we have the Kirchhoff equations for the cycles VWYV and WZYW, then we can deduce the equation for the cycle VWZYV. It will save a lot of work if we can find a set of cycles that gives us the information we need without any redundancy, and this can be done by using a fundamental set of cycles.
In this example, taking the fundamental system of cycles in Fig. (3.90), we obtain the following equations.