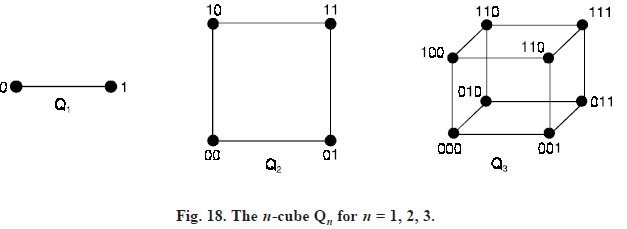
N-cube

N-cube: The N-cube denoted by Qn, is the graph that has vertices representing the 2n bit strings of length n. Two vertices are adjacent if and only if the bit strings that they represent differ in exactly one bit position. The graphs Q1, Q2, Q3 are displayed in Figure 18. Thus Qn has 2n vertices and n . 2n – 1 edges, and is regular of degree n.

Problem 1.. Determine whether the graphs shown is a simple graph, a multigraph, a pseudograph.

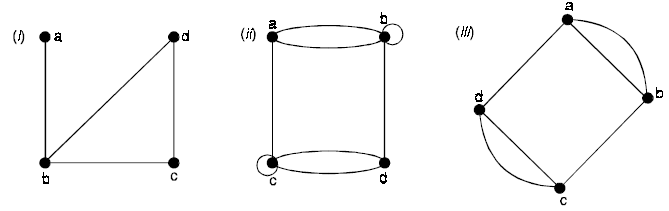
Solution.

(i) Simple graph
(ii) Pseudograph
(iii) Multigraph.

Problem 2. Consider the following directed graph G : V(G) = {a, b, c, d, e, f, g} E(G) = {(a, a), (b, e), (a, e), (e, b), (g, c), (a, e), (d, f), (d, b), (g, g)}.
(i) Identify any loops or parallel edges.
(ii) Are there any sources in G ?
(iii) Are there any sinks in G ?
(iv) Find the subgraph H of G determined by the vertex set V ′ = {a, b, c, d}.

Solution.

(i) (a, a) and (g, g) are loops (a, a) and (a, e) are parallel edges.
(ii) No sources
(iii) No sinks
(iv) V′ = {a, b, c, d}
     E′ = {(a, a), (d, b)}
     H = H(V′, E′).

Problem 3. Consider the following graphs, determine the (i) vertex set and (ii) edge set.

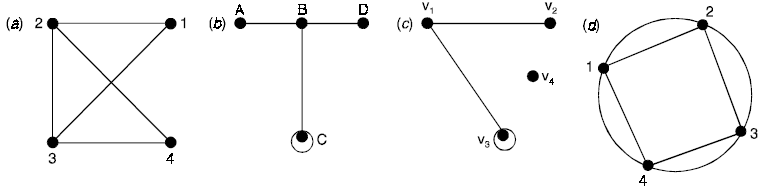
Solution.

(a) (i) Vertex set V = {1, 2, 3, 4},
     (ii) Edge set E = {(1, 2), (1, 3), (2, 3), (2, 4), (3, 4)}
(b) (i) Vertex set V = {A, B, C, D}
     (ii) Edge set E = {(A, B), (B, C), (B, D), (C, C)}

(c) (i) Vertex set V = {v1, v2, v3, v4}
     (ii) Edge set E = {(v1, v2), (v1, v3), (v3, v3)}
(d) (i) Vertex set V = {1, 2, 3, 4}
     (ii) Edge set E = {(1, 2), (2, 3), (3, 4), (4, 1)}

All edges are double edges.