Partitions And Factorization

PARTITIONS: The degrees d1, ..... dP of the points of a graph form a sequence of non-negative integers, whose sum is of course 2q. In number theory, to define a partition of a positive integer n as a list or unordered sequence of positive integers whose sum is n.
For example, 4 has five partitions
4, 3 1, 2 2, 2 1 1, 1 1 1 1.
The degrees of a graph with no isolated points determine such a partition of 2q.

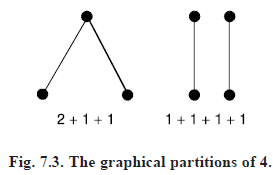
The partition of a graph is the partition of 2q as the sum of the degrees of the points 2q = Σdi. A partition Σdi of n into P parts is graphical if there is a graph G whose points have degree di. If such a partition is graphical then certainly every di ≤ P – 1 and n is even.

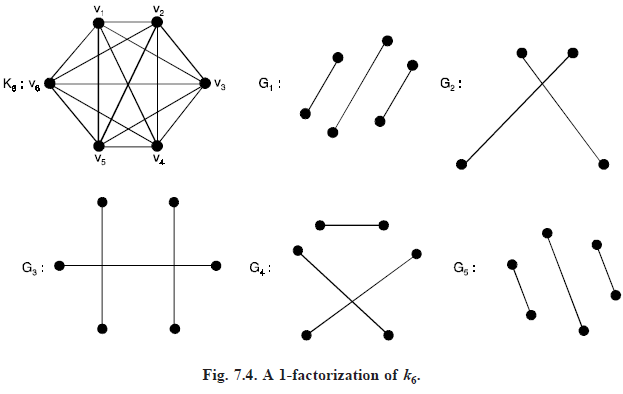
1-FACTORIZATION
A factor of a graph G is a spanning subgraph of G which is not totally disconnected. We say that G is the sum of factors Gi if it is their line-disjoint union and such a union is called a factorization of G. If G is the sum of n-factors their union is called an n-factorization and G it self is n-factorable. When G has a 1-factor, say G1, it is clear that P is even and the lines of G1 are point disjoint. In particular, K_{2n 1} cannot have a 1-factor but K_2n certainly can.

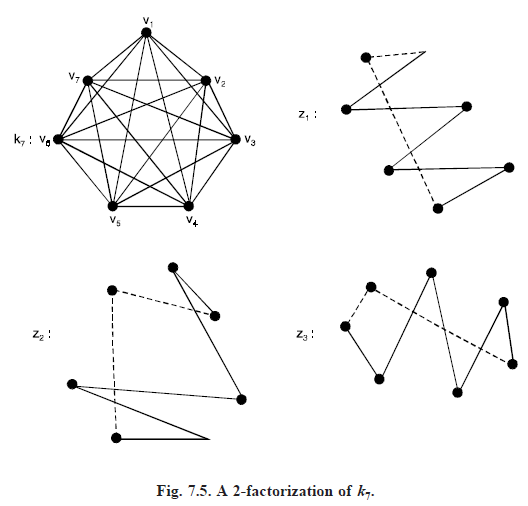
2-FACTORIZATION
If a graph is 2-factorable then each factor must be a union of disjoint cycles. If a 2-factor is connected, it is a spanning cycle. We saw that a complete graph is 1-factorable if and only if it has even number of points. Since a 2-factorable graph must have all points even, the complete graphs K2n are not 2-factorable. The odd complete graphs are 2-factorable and infact a stronger statement can be made.