Planer Graphs

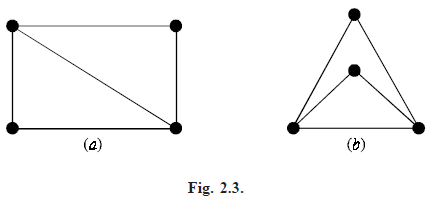
PLANAR GRAPHS: A graph G is said to be planar if there exists some geometric representation of G which can be drawn on a plane such that no two of its edges intersect. The points of intersection are called crossovers. A graph that cannot be drawn on a plane without a crossover between its edges crossing is called a plane graph. The graphs shown in Figure 2.3(a) and are planar graphs.

A drawing of a geometric representation of a graph on any surface such that no edges intersect is called embedding.

Note that if a graph G has been drawn with crossing edges, this does not mean that G is non planar, there may be another way to draw the graph without crossovers. Thus to declare that a graph G is non planar. We have to show that all possible geometric representations of G none can be embedded in a plane.

Equivalently, a graph G is planar is there if there exists a graph isomorphic to G that is embedded in a plane, otherwise G is non planar.

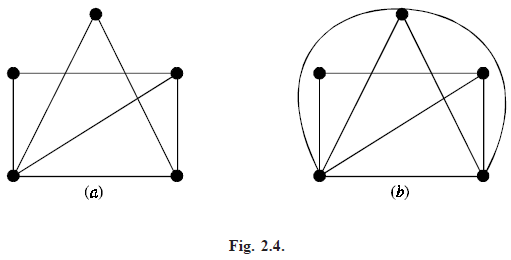
For example, the graph in Figure 2.4(a) is apparently non planar. However, the graph can be redrawn as shown in Figure (2.4)(b) so that edges don’t cross, it is a planar graph, though its appearance is non coplanar.