Prim’s Algorithm
Prim’s algorithm: Let G = (V, E) be a connected graph with | V | = n. To find the adjacency matrix for G. Now proceed according to the following steps :
Step 1 : Select a vertex v1 ∈ V and arrange the adjacency matrix of the graph in such a way that the first row and first column of the matrix corresponds to V1.
Step 2 : Choose a vertex v2 of V such that (v1, v2) ∈ E. Merge v1 and v2 into a new vertex, call it vmi and drop v2. Replace v1 by vmi in the graph. Find the new adjacency matrix corresponding to this new quotient graph.
Step 3 : While merging select an edge from those edges which are going to be removed (or merged with other edge) from the graph. Keep a record of it.
Step 4 : Repeat steps 1, 2 and 3 until all vertices have been merged into one vertex.
Step 5 : Now construct a tree from the edges, collected at different iterations of the algorithm. The same Prim’s algorithm with little modification can be used to find a minimum spanning tree for a weighted graph. The stepwise algorithm is given below.
Let G = (V, E) be graph and S = (Vs, Es) be the spanning tree to be found from G.
Step 1 : Select a vertex v1 of V and initialize
Vs = {v1} and Es = {}
Step 2 : Select a nearest neighbour of vi from V that is adjacent to same vj ∈ Vs and that edge (vi, vj) does not form a cycle with members edge of Es.
Set Vs = Vs ∪ {vi} and
Es = Es ∪ {(vi, vj)}
Step 3 : Repeat step 2 until | Es | = | V | – 1.
Theorem 4.5. Prim’s algorithms produces a minimum spanning tree of a connected weighted graph.
Proof. Let G be a connected weighted graph.
Suppose that the successive edges chosen by Prim’s algorithm are e1, e2, ..., en – 1. Let S be the tree with e1, e2, ..., en – 1 as its edges, and let Sk be the tree with e1, e2, ..., ek as its edges.
Let T be a minimum spanning tree of G containing the edges e1, e2, ..., ek, where k is the maximum integer with the property that a minimum spanning tree exists containing the first k edges chosen by Prim’s algorithm. The theorem follows if we can show that S = T.
Suppose that S ≠ T, so that k < n – 1.
Consequently, T contains e1, e2, ..., ek, but not ek 1.
Consider the graph made up of T together with ek 1.
Since this graph is connected and has n edges, too many edges to be a tree, it must contain a simple circuit.
This simple circuit must contain ek 1 since there was no simple circuit in T.
Furthermore, there must be an edge in the simple circuit that does not belong to Sk 1 since Sk 1 is a tree.
By starting at an end point of ek 1 that is also an endpoint of one of the edges e1, ..., ek, and following the circuit until it reaches an edge not in Sk 1, we can find an edge e not in Sk 1 that has an end point that is also an end point of one of the edges e1, e2, ..., ek.
By deleting e from T and adding ek 1, we obtain a tree T′ with n – 1 edges (it is a tree since it has no simple circuits).
Note that the tree T′ contains e1, e2, ..., ek, ek 1.
Furthermore, since ek 1 was chosen by Prim’s algorithms at the (k 1)st step, and e was also available at that step, the weight of ek 1 is less than or equal to the weight of e.
From this observation it follows that T′ is also a minimum spanning tree, since the sum of the weights of its edges does not exceed the sum of the weights of the edges of T.
This contradicts the choice of k as the maximum integer so that a minimum spanning tree exists containing e1, ..., ek.
Hence, k = n – 1 and S = T.
It follows that Prim’s algorithm produces a minimum spanning tree.
Problem . Find the minimum spanning tree for the weighted graph of the Figure (4.29).
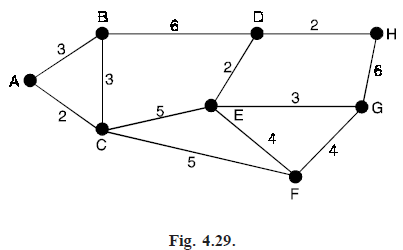
Solution. Let is begin with the node A of the graph.
Let S = (Vs, Es) be the spanning tree to be found from G. Initialize Vs = {A} and Es = { }.
There are eight nodes so the spanning tree will have seven arcs.
The iterations of algorithm applied on the graph are given below. The number indicates iteration number.
1. Nodes B and C are neighbours of A. Since node C is nearest to the node A we select C. Thus, we have Vs = {A, C} and Es = {(A, C)}.
2. Now node B is neighbour of both A and C and C has nodes E and F as its neighbour. We have AB = 3, CB = 3, CE = 5, and CF = 5.
Thus, the nearest neighbour is B. We can select either AB or CB. We select CB.
Therefore, Vs = {A, C, B} and Es = {(A, C), (C, B)}.
3. Now D, E, F are neighbour of nodes in Vs. An arc AB is still to be considered. This arc forms cycle with arcs AC and CB already in Es so it cannot be selected. Thus, we have to select from BD = 6, CE = 5, CF = 5.
We may take either CE or CF. We select CF. Therefore, Vs = {A, C, B, F} and Es = {(A, C), (C, B), (C, F)}
4. Now we have to select an arc from BD = 6, CE = 5, FE = 4, FG = 4. We select FE. Therefore, Vs = {A, C, B, F, E} and Es = {(A, C), (C, B), (C, F), (F, E)}.
5. The selection of arc CE is ruled out as it forms a cycle with the edges CF and FE. Thus, we have to select an arc from BD = 6, ED = 2, FG = 4. We select ED. Therefore, Vs = {A, C, B, F, E, D} and
Es = {(A, C), (C, B), (C, F), (F, E), (E, D)}.
6. Now BD is ruled out as it forms cycle with CB, CF, FE and ED. Thus we have to consider DH = 2, EG = 3, FG = 4. We select DH. Therefore Vs = {A, C, B, F, E, D, H} and Es = {(A, C), (C, B), (C, F), (F, E), (E, D), (D, H)}.
7. Now left over arcs are EG = 3, HG = 6, FG = 4. We select EG. Therefore, Vs = {A, C, B, F, E, D, H, G} and
Es = {(A, C), (C, B), (C, F), (F, E), (E, D), (D, H), (E, G)}.
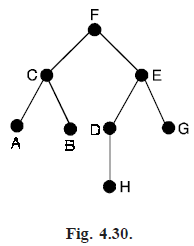
Since number of edges in Es is seven process terminates here. The spanning tree so obtained is shown in the Fig. (4.30).