Problem Of Seating Arrangement

PROBLEM OF SEATING ARRANGEMENT : Nine members of a club meet every day for a dinner. They sit in a round table for a dinner, but no two members who sat together will sit together in future. How long is this possible ?

Solution. The seating arrangement can be represented as follows :

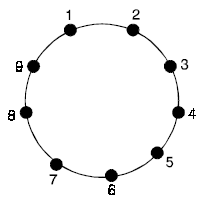
Any two numbers can occupy consecutive tables. The neighbouring persons can be represented by an edge. Then each arrangements is a cycle on 9 vertices. These cycles can be chosen from k9 (since each member can sit with anybody in the beginning).

Thus distinct arrangements as they desired are the edge disjoint (no edges should re-appear, i.e., none of the persons sitting together will sit together in next arrangements) Hamiltonian cycles of K9, which is possible only for four days (as 9 = 2n 1 ⇒ n = 4). However this is also possible for 10 members for 4 days only.

If we consider a bench instead of a round table, then for 10 members it is possible for 5 days. (Hamiltonian paths of k10). What can you say about the same situation for nine members.