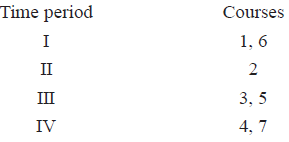Scheduling Final Exams

Scheduling Final Exams : How can the final exams at a university be scheduled so that no student has two exams at the same time ?
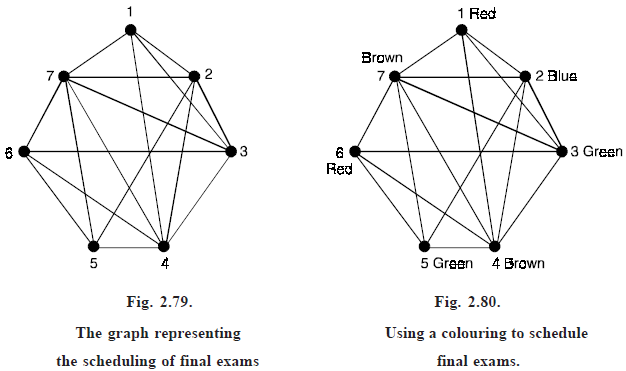
Solution. This scheduling problem can be solved using a graph model, with vertices representing courses and with an edge between two vertices if there is a common student in the courses they represent. Each time slot for a final exam is represented by a different colour. A scheduling of the exams corresponds to a colouring of the associated graph. For instance, suppose there are seven finals to be scheduled. Suppose the courses are numbered 1 through 7. Suppose that the following pairs of courses have common students : 1 and 2, 1 and 3, 1 and 4, 1 and 7, 2 and 3, 2 and 4, 2 and 5, 2 and 7, 3 and 4, 3 and 6, 3 and 7, 4 and 5, 4 and 6, 5 and 6, 5 and 7, and 6 and 7.

In Figure 2.79, the graph associated with this set of classes is shown.
A scheduling consists of a colouring of this graph.
Since the chromatic number of this graph is 4, four times slots are needed. A colouring of the graph using four colours and the associated schedule are shown in Figure 2.80.