Semi Walk Paths And Circuits And Tournaments

SEMI-WALK, SEMI-PATH, SEMI-CIRCUIT

Semi-Walk: A semi-walk in a digraph D is a walk in the underlying graph of D, but is not a directed walk in D. A walk in D can mean either a directed walk or a semi-walk in D.

Semi-path: A semi-path in a digraph D is a path in the underlying graph of D, but is not a directed path in D. A path in D can mean either a directed path or a semi-path in D.

Semi-circuit: A semi-circuit in a digraph D is a circuit in the underlying graph of D, but is not a directed circuit in D. A circuit in D can mean either a directed circuit or a semi-circuit in D.
For example, in the digraph in Fig. (8.1), the sequence v6e6v1e9v2e4v5 is a semi-path and the sequence v5e5v2e1v1e8v5 is a semi-circuit.

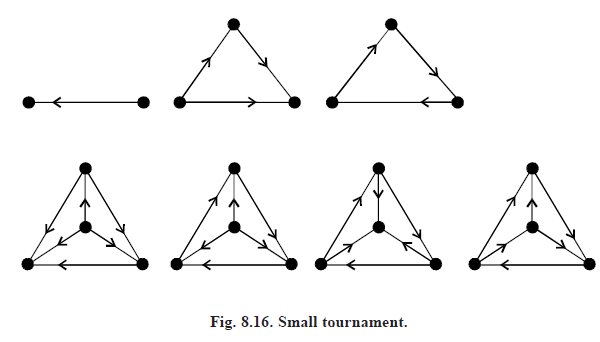
TOURNAMENTS: A tournament is an oriented complete graph. All tournaments with two, three and four points are shown in Fig. 8.16.

The first with three points is called a transitive triple, the second a cycle triple.