Spanning Tree

Introduction: A spanning tree is a spanning subgraph, that is a tree. In Other words a spanning tree for a connected graph G is a subgraph of G that is a tree and whose vertex set is all the vertices of G. If G is a tree then it has only one spanning tree, G itself. If G is not a tree it has more than one spanning tree.

Consider the following problem. In the diagram shown below we have four wells in an offshore oilfield (nodes 1 to 4 below) and an on-shore terminal (node 5 below). The four wells in this field must be connected together via a pipeline network to the on-shore terminal.

The various pipelines that can be constructed are shown as links in the diagram below and the cost of each pipeline is given next to each link. What pipelines would you recommend be built?

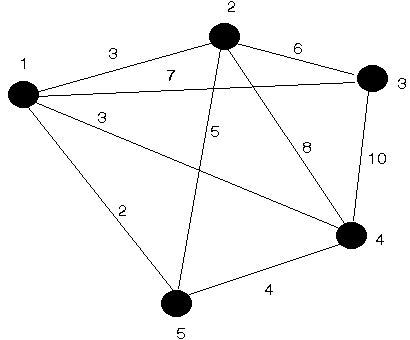
It is clear that this particular problem is a specific example of a more general problem - namely given a graph (such as that shown above) which links would we use so that:

• the total cost of the links used is a minimum; and
• all the points are connected together.

This problem is called the shortest spanning tree (SST) problem. Note here that the phrase "minimal spanning tree" (MST) is also often used instead of the phrase "shortest spanning tree" (SST).

For example, in the diagram above, one possible structure connecting all the points together would consist of the links 1-2, 2-3, 3-4, 4-5 and 5-1, but there are other structures where the total cost of the links used is smaller than in this structure (e.g. drop any link in the circle (cycle) 1-2-3-4-5-1 formed above).

Points to note :

• for an n-node graph the solution involves (n-1) links
• the solution can be easily arrived at by using an algorithm due to Kruskal (developed in the mid 1950's)
• the final structure is called the shortest spanning tree (SST) of the graph.

Branch of tree: An edge in a spanning tree T is called a branch of T.

Chord: An edge of G that is not in a given spanning tree is called a chord.

Note :
(1) The branches and chords are defined only with respect to a given spanning tree.
(2) An edge that is a branch of one spanning tree T1 (in a graph G) may be chord, with respect to another spanning tree T2.