Storage Representation Of Binary Tree

STORAGE REPRESENTATION OF BINARY TREE: In this section, we discuss two ways of representing a binary tree in computer memory. The first way uses a single array, called the sequential representation of binary tree. The second is called the link representation.

Sequential Representation: We can represent the vertices of a binary tree as array elements and access the vertices using array notations. The advantage is that we need not use a chain of pointers connecting the widely separated vertices.

Consider the almost complete binary tree shown in Fig. 3.39.

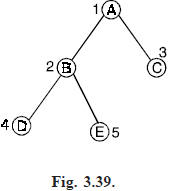
Note that we assigned numbers for all the nodes. We can assign numbers in such a way that the root is assigned the number 1, a left child is assigned twice the number assigned to its father, a right child is assigned one more than twice the number assigned to its father. We can keep the vertices of an almost complete binary tree in an array Fig. (3.40) shows vertices kept in an array.

Arrray positions vertices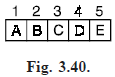

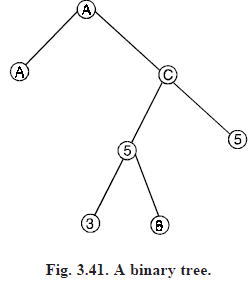
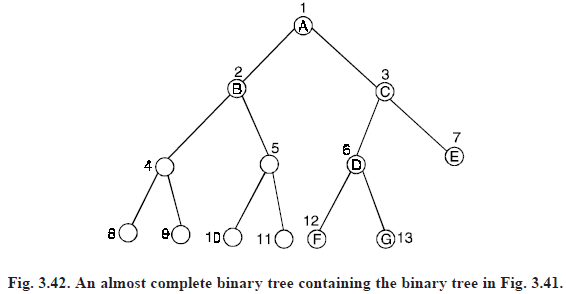
By this convention, we can map vertex i to ith index in the array, and the parent of vertex i will get mapped at an index i/2 where as left child of vertex i gets mapped at an index 2i and right child gets mapped at an index 2i 1. The sequential representation can be extended to general binary trees. We do this by identifying an almost complete binary tree that contains the binary tree being represented. An almost complete binary tree containing the binary tree in Fig. (3.41) is shown in Fig. (3.42).

 

 

 

 

 

 

 

 

 

Linked representation: An array representation of a binary tree is not suitable for frequent insertions and deletions, and therefore we find that even though no storage is wasted if the binary tree is a complete one when array representation is used, it makes insertion and deletion is a tree is costly.

Computer representation of trees based on linked allocation seems to more popular because of the ease with which nodes can be inserted in and deleted from a tree, and because tree structure can grow to an arbitary size. Therefore instead of using an array representation, one can use a linked representation, in which every node is represented as a structure having 3 fields, one for holding data, one for linking it with left sub-tree and the one for linking it with right sub-tree as shown below. A general tree can easily be converted into an equivalent binary tree by using the natural correspondence algorithm. Where LLINK or RLINK contain a pointer to the left sub-tree respectively of the node in question. DATA contains the information which is to be associated with this particular node. Each pointer can have a value of NULL.
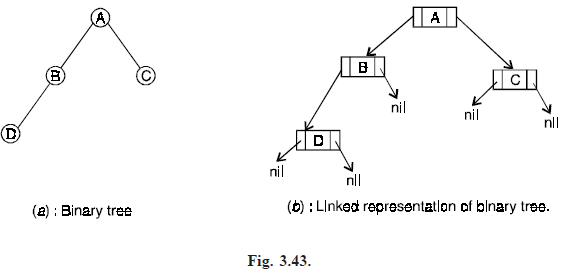
An example of binary tree as a graph and its corresponding linked representation in memory are given in Fig. (3.43).