Subdivision Graphs And Inner Vertex Sets

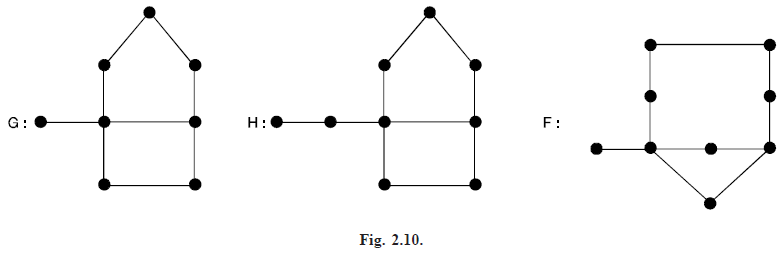
SUBDIVISION GRAPHS: A subdivision of a graph is a graph obtained by inserting vertices (of degree 2) into the edges of G. For the graph G of the figure below, the graph H is a subdivision of G, while F is not a subdivision of G.

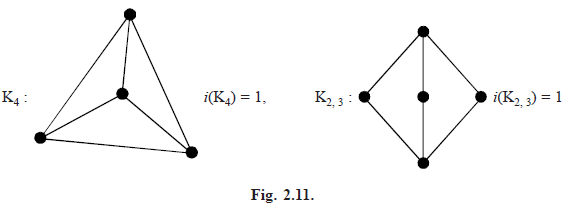
INNER VERTEX SET: A set of vertices of a planar graph G is called an inner vertex set I(G) of G. If G can be drawn on the plane in such a way that each vertex of I(G) lies only on the interior region and I(G) contains the minimum possible vertices of G. The number of vertices i(G) of I(G) is said to be the inner vertex number if they lie in interior region of G.

For any cycle Cp, i(Cp) = 0.