Transversal Theory
TRANSVERSAL THEORY
Transversal: If E is a non empty finite set, and if F = (S1, ..... Sm) is a family of (not necessarily distinct) nonempty subsets of E, then a transversal of F is a set of m distinct elements of E, one chosen from each set Si.
Suppose that E = {1, 2, 3, 4, 5, 6} and Let S1 = S2 = {1, 2}, S3 = S4 = {2, 4}, S5 = {1, 4, 5, 6}
Then it is impossible to find five distinct elements of E, one from each subset Si ; In otherwords, the family F = (S1, ....., S5) has no transversal. The subfamily F′ = (S1, S2, S3, S4, S5) has a transversal. For example, {1, 2, 3, 4, 5}.
Partial transversal: A transversal of a subfamily of F a partial transversal of F. For example, {1, 2, 3, 4}, here F has several partial transversal, such as, {1, 2, 3, 6}, {2, 3, 6}, {1, 5}, and φ.
We note that any subset of a partial transversal is a partial transversal.
Note : A given family of subsets of a set has a transversal. The connection between this problem and the marriage problem is easily seen by taking E to be the set of boys, and Si to be the set of boys known by girl gi, for 1 ≤ i ≤ m. A transversal in this case is then simply a set of m boys, one corresponding to, and known by, each girl.
Marriage problem: If there is a finite set of girls, each of whom knows several boys, under what conditions can all the girls marry the boys in such a way that each girl marries a boy she knows ?
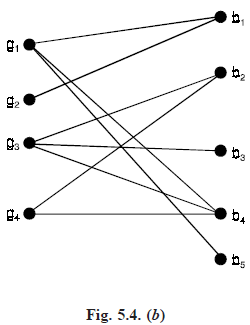
For example. If there are four girls {g1, g2, g3, g4} and five boys {b1, b2, b3, b4, b5} and the friendships are as shown in Figure 5.4(a) and (b), below

then a possible solution is for g1 to marry b4, g2 to marry b1, g3 to marry b3, and g4 to marry b2. This problem can be represented graphically by taking G to be the bipartite graph in which the vertex set is divided into two disjoint sets V1 and V2, corresponding to the girls and boys, and where each edge joins a girl to a boy she knows. Figure 5.4(b) shows the graph G corresponding to the situation of Figure 5.4(a).
In graph-theoretic form: If G = G(V1, V2) is a bipartite graph, when does there exist a complete matching from V1 to V2 in G ?
Marriage Condition: A ‘‘matrimonial terminology’’, we note that, for the solution of the marriage problem, every k girls must know collectively at least k boys, for all integers k satisfying 1 ≤ k ≤ m, where m denotes the total number of girls. We refer to this condition as the marriage condition. It is a necessary condition and it turns out to be sufficient.
Common transversals: If E is a non-empty finite set and F = (S1, ......, Sm) and G = (T1, ......, Tm) are two families of nonempty subsets of E, it is of interest to know when there exists a common transversal for F and G. i.e., a set of m distinct elements of E that forms a transversal of both F and G. For example, In time tabling problems, E may be the set of times at which lectures can by given, the sets Si may be the times that m given professors are willing to lecture, and the sets Ti may be the times that m lecture rooms are available. Then the finding of a common transversal of F and G enables us to assign to each professor an available lecture root at a suitable time.
Latin squares: An m × n latin rectangle is an m × n matrix M = (mij) whose entries are integers satisfying
(i) 1 ≤ mij ≤ n (ii) no two entries in any row or in any column are equal.
We note that (i) and (ii) imply that n ≤ n.
If m = n, then the latin rectanle is a latin square.
For example, Figure 5.5(a) and 5.5(b) shows a 3 × 5 latin rectangle and a 5 × 5 latin square.
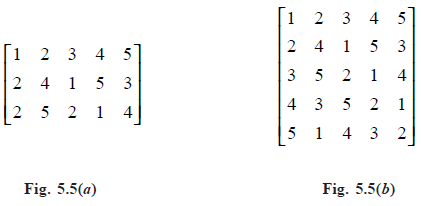
(0, 1) – matrices: The way of studying transversals of a family F = (S1, ......, Sm) of non-empty subsets of a set E = {e1, ......, en} is to study the incidence matrix of the family, the m × n matrix A = (aij) in which aij = 1 if ej ∈ Si and aij = 0 otherwise. We call such a matrix, in which each entry is 0 or 1, a(0, 1) – matrix.
Note : If the term rank of A is the largest number of 1s of A, no two of which lie in the same row or column, then F has a transversal if and only if the term rank of A is m. Moreover, the term rank of A is precisely the number of elements in a partial transversal of largest possible size.
Edge-disjoint paths: The number of paths connecting two given vertices v and w in a graph G. We may ask for the maximum number of paths from v to w, no two of which have an edge in common, such paths are called edge-disjoint paths.
Vertex-disjoint paths: The number of paths connecting two given vertices v and w in a graph G. We may ask for the maximum number of paths from v to w, no two of which have a vertex in common, such paths are called vertex-disjoint paths. For example, in the graph of Fig. (5.6), there are four edge-disjoint paths are two vertex-disjoint ones.
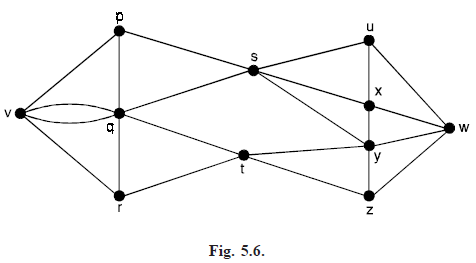
vw-disconnecting set: Assume that G is a connected graph and that v and w are distinct vertices of G. A vw-disconnecting set of G is a set E of edges of G such that each path from v to w includes an edge of E. We note that a vw-disconnecting set is a disconnecting set of G.
vw-separating set: Assume that G is a connected graph and that v and w are distinct vertices of G. A vw-separating set of G is a set S of vertices, other than v or w, such that each path from v to w passes through a vertex of S.
In Fig, (5.6), the sets E1 = {ps, qs, ty, tz} and E2 = {uw, xw, yw, zw} are vw-disconnecting sets, and V1 = {s, t} and V2 = {p, q, y, z} are vw-separating sets.