Traversing Binary Trees

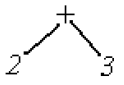
Traversing Binary Trees: Yet another use for a binary tree is to represent arithmetic operations, such as 2 3, or 6*3-1. We can represent these in a binary tree and then traverse and interpret the results in a variety of ways. The notations we will examine place values at terminal nodes and operators in internal nodes. For example, we can represent the expression 2 3 using a binary tree like this:

Similarly, we can represent the expression 6*3-1 using a binary tree this way.

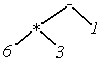
In this case, we are going to process the multiplication first. Like a tournament, the last operation goes in the root node.
In order to make sense of the tree we must establish how we are going to examine and process the information in the nodes. There are three methods.

In-fix / In-order
Traversing a binary tree using infix or in-order produces a sequence of values and operators almost identical to what we started with. Start from the upper left side of the root node, and completely trace the outside edge of the tree and the nodes. With in-fix / in-order, the node content is recognized / processed as you pass to the right, going underneath the node. You can stop when you get to the right side of the root node. In the case of the first tree, we get this:

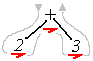
2 3

In the second tree, we get this sequence:

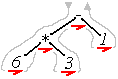
6 * 3 - 1

Notice that the operator can be directionally sensitive (which is to say, as in subtraction, what gets subtracted from what changes the answer).

Parentheses and Precedence: We got lucky in the last example. If we were to simply reorder the operators in the expression to 1-6*3, we would get a very different result. As you can see, we would be subtracting 6 from 1, and then multiplying by 3. Precedence is the method in which, some operators get processed before others. In this case, multiplication and division get processed before addition and subtraction.
We can also force precedence by grouping an expression in a set of parentheses. The expression 3*(6-1) forces us to process the subtraction before the multiplication.
Precedence functions this way by implying grouping. Thus, the way most of us learned arithmetic, higher precedent functions like multiplication and division are automatically recognized, but computers require that we be more explicit. For this reason, one thing that some expression processors do is parenthesize based on precedence. This allows another part of the program to ignore the problem of precedence completely and just pay attention to grouping with parentheses. Thus, our original expression, 6*3-1, would be rewritten as ((6*3)-1). While the last set of parentheses may seem excessive, it also doesn’t hurt.

Prefix / Pre-order: Traversing a binary tree using prefix or pre-order means to trace the outline of the tree, again starting from the upper left next to the root, identifying nodes as you travel downward on the left side of the node. Thus, the first node is always the root node. Here is an example of the tree using 2 3:

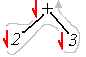
2 3

A way to interpret this is linguistically; add the values of two and three. Obviously things get more complicated (and un-earthly?) as the expression gets more complicated. Here is our other example:

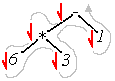
- * 6 3 1
“Subtract the result of multiplying 6 and 3 by 1”. (I didn’t say it would make sense to us, but it might make sense to a computer.)

Polish Notation: This notation was discovered in the 1920’s by Jan Lukasiewicz, a Polish mathematician. One of the useful properties of this notation is that it can be processed by a computer or other computing machine. How do you think it might work?