Trees And Sorting

TREES AND SORTING

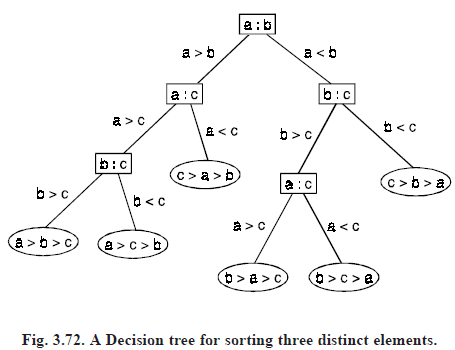
Decision trees: Rooted trees can be used to model problems in which a series of decisions leads to a solution. For instance, a binary search tree can be used to locate items based on a series of comparisons, where each comparison tells us whether we have located the item, or whether we should go right or left in a subtree. A rooted tree in which each internal vertex corresponds to a decision, with a subtree at these vertices for each possible outcome of the decision, is called a decision tree. The possible solutions of the problem correspond to the paths to the leaves of this rooted tree.

The complexity of sorting algorithms: Many different sorting algorithms have been developed. To decide whether a particular sorting algorithm is efficient, its complexity is determined. Using decision trees as models, a lower bound for the worst-case complexity of sorting algorithms can be found. We can use decision trees to model sorting algorithms and to determine an estimate for the worst-case complexity of these algorithms.

Note that given n elements, there are n ! possible orderings of these elements, since each of the n ! permutations of these elements can be the correct order. The sorting algorithms are based on binary comparisons, that is, the comparison of two elements at a time. The result of each such comparison narrows down the set of possible orderings.

Thus, a sorting algorithms based on binary comparisons can be represented by a binary decision tree in which each internal vertex represents a comparison of two elements. Each leaf represents one of the n ! permutations of n elements.

The merge sort algorithms
For sorting a given list of n items into ascending order. The method is called the merge sort, and we find that the order of its worst-case time-complexity function is 0/(n log2 n). This will be accomplished in the following manner.
(i) First we measure the number of comparisons needed when n is a power of 2. Our method will apply a pair of balanced complete binary trees.
(ii) Then we cover the case for general n by using optional material on divide and conquer alorithms, where
(a) The time to solve the intial problem of size n = 1 is a constant c ≥ 0 (solving the problem for a small value of ‘n’ directly).
(b) The time to break the given problem of size n into a smaller (similar) problems, together with the time to combine the solutions of these smaller problems to get a solution for the given problem, is h(n), a function of n.

For the case where n is an arbitrary positive integer, we start by considering the following procedure.
Given a list of n items to sort into ascending order, the merge sort recursively splits the given list and all subsequent sublists in half until each sublist contains a single element. Then the procedure merges these sublists in ascending order until the original n items have been so sorted. The splitting and merging processes can best be described by a pair of balanced complete binary trees.

Merge sort algorithm
Procedure :
Step 1 : If n = 1, then list is already sorted and the process terminates. If n > 1, then go to step (2).
Step 2 : (Divide the array and sort the subarrays). Perform the following :
(i) Assign m the value [n/2]
(ii) Assign to List 1 the subarray List [1], List [2], ...... List [m].
(iii) Assign to List 2 the subarray List [m 1], List [m 2], ......, List [n].
(iv) Apply merge sort to List 1 (of size m) and to List 2 (of size n – m).
Step 3 : Merge (List 1, List 2).