Types Of Enumeration

Introduction: Cayley’s (1857) classic paper, a great deal of work has been done on enumeration (also called counting) of different types of graphs, and the results have been applied in solving some practical problems.

The Pioneers is graphical enumeration theory were Cayley, Redfield and Pólya. Graphical enumeration methods in current use were anticipated in the unique paper by Redfield pubished in 1927 Enumerative techniques will be developed and used for counting certain types of graphs. A thorough exposition of Pólya’s counting theorem, the most powerful tool in graph enumeration.

Types of Enumeration

Type 1. Counting the number of different graphs (or digraphs) of a particular kind. For example, all connected, simple graphs with eight vertices and two circuits.

Type 2. Counting the number of subgraphs of a particular type in a given graph G, such as the number of edge-disjoint paths of length k between vertices a and b in G.
In problems of type 1 the word ‘different’ is of utmost importance and must be clearly understood. If the graphs are labeled, i.e., each vertex is assigned a name distinct from all others, all graphs are counted on the otherhand, in the case of unlabeled graphs the word ‘different’ means non-isomorphic, and each set of isomorphic graphs is counted as one.
For example, let us consider the problem of constructing all simple graphs with n vertices and e edges. There are unordered pairs of vertices. If we regard the vertices as distinguishable from one another i.e., labeled graphs, there are 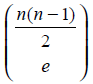ways of selecting e edges to form the graph.
Thus 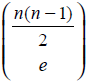gives the number of simple labeled graphs with n vertices and e edges.

In the problems of type 2, usually involves a matrix representation of graph G and manipulations of this matrix. Such problems, although after encountered in practical applications, are not as varied and interesting as those in the first category.