Types Of Graphs

TYPES OF GRAPHS: Some important types of graph are introduced here.

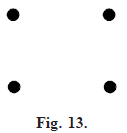
Null graph: A graph which contains only isolated node, is called a null graph. i.e., the set of edges in a null graph is empty. Null graph is denoted on n vertices by Nn. N4 is shown in Figure (13), Note that each vertex of a null graph is isolated.

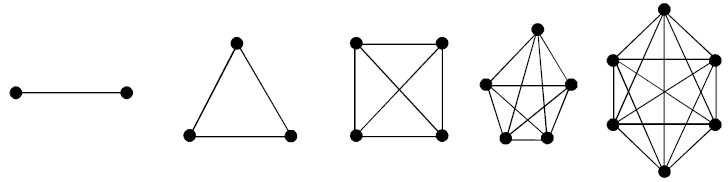
Complete graph: A simple graph G is said to be complete if every vertex in G is connected with every other vertex. i.e., if G contains exactly one edge between each pair of distinct vertices. A comple graph is usually denoted by Kn. It should be noted that Kn has exactly {n (n-1)/2} edges.
The graphs Kn for n = 1, 2, 3, 4, 5, 6 are show in Figure 14.

Regular graph: A graph in which all vertices are of equal degree, is called a regular graph. If the degree of each vertex is r, then the graph is called a regular graph of degree r. Note that every null graph is regular of degree zero, and that the complete graph Kn is a regular of degree n – 1. Also, note that, if G has n vertices and is regular of degree r, then G has edges.

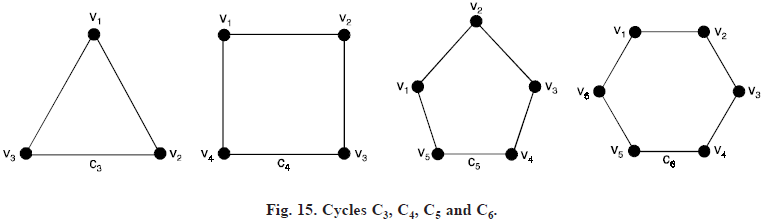
Cycles: The cycle Cn, n ≥ 3, consists of n vertices v1, v2, ......, vn and edges {v1, v2}, {v2, v3}, ......, {vn – 1, vn}, and {vn, v1}. The cyles c3, c4, c5 and c6 are shown in Figure 15.

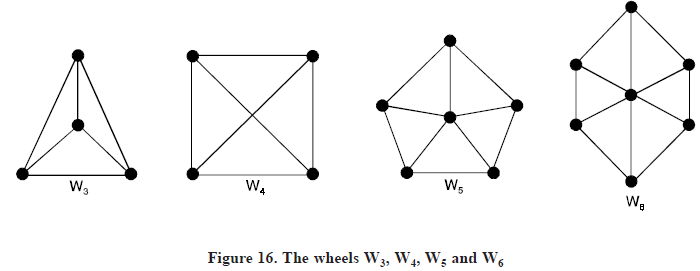
Wheels: The wheel Wn is obtained when an additional vertex to the cycle cn, for n ≥ 3, and connect this new vertex to each of the n vertices in cn, by new edges. The wheels W3, W4, W5 and W6 are displayed in Figure 16.

Platonic graph: The graph formed by the vertices and edges of the five regular (platonic) solids—The tetrahedron, octahedron, cube, dodecahedron and icosahedron. The graphs are shown in Figure 17.