Types Of Matroid
Types of Matroid
Bipartite matroid: A bipartite matroid be a matroid, in which each cycle has an even number of elements.
Eulerian matroid: A matroid on a set E to be an Eulerian matroid if E can be written as a union of disjoint cycles.
Discrete matroids: At the other extreme is the discrete matroid on E, in which every subset of E is independent. The discrete matroid on E has only one base, E itself, and that the rank of any subset A is the number of elements in A.
Trivial matroids: Given any non-empty finite set E, we can define on it a matroid whose only indepenent set is the empty set φ. This matroid is the trivial matroid on E and has rank O.
Uniform matroids: The k-uniform matroid on E, whose bases are those subsets of E with exactly k elements, the trivial matroid on E is o-uniform and the discrete matroid is | E |-uniform. We note that the independent sets are those subsets of E with not more than k elements, and that the rank of any subset A is either | A | or k.
Isomorphic matroids: Two matroids M1 and M2 to be isomorphic if there is a one-one correspondence between their underlying sets E1 and E2 that preserves independence. Thus, a set of elements of E1 is independent in M1 if and only if the corresponding set of elements of E2 independent in M2.
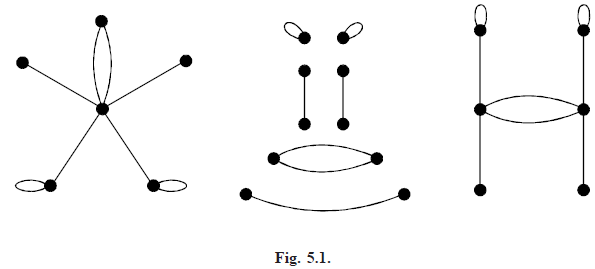
For example, the cycle matroids of the three graphs in Figure below are all isomorphic.
We note that, although matroid isomorphism preserves cycles, cutsets and the number of edges in a graph, it does not necessarily preserve connectedness, the number of vertices, or their degrees.
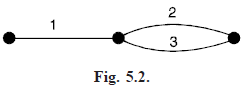
Graphic matroids: A matroid M(G) on the set of edges of a graph G by taking the cycles of G as the cycles of the matroid. M(G) is the cycle matroid of G and its rank function is the cutset rank ξ. It is natural to ask whether a given matroid M is the cycle matroid of some graph. In otherwords, does there exists a graph G such that M is isomorphic to M(G) ? Such matroids are called graphic matroids.
For example, the matroid M on the set {1, 2, 3} whose bases are {1, 2} and {1, 3} is a graphic matroid isomorphic to the cycle matroid of the graph in Figure below.
Cographic matroids: Given a graph G, the cycle matroid M(G) is not the only matroid that can be defined on the set of edges of G. Because of the similarity between the properties of cycles and of cutsets in a graph, we can construct a matroid by taking the cutsets of G as cycles of the matroid. We call it the cutset matroid of G, denoted by M*(G). We note that a set of edges of G is independent if and only if it contains no cutset of G. We call a matroid M cographic if there exists a graph G such that M is isomorphic to M*(G).
Planar matroids: A matroid that is both graphic and cographic is a planar matroid.
Transversal matroids: If E is a non-empty finite set and in F = (S1, ...... Sm) is a family of non-empty subsets of E, then the partial transversals of F can be taken as the independent sets of a matroid on E, denoted by M(F) or M(S1, ......, Sm). Any matroid obtained in this way is a transversal matroid.
For example, the above graphic matroid M is a transversal matroid on the set {1, 2, 3}, since its independent sets are the partial transversal of the family F = (S1, S2), where S1 = {1} and S2 = {2, 3}. We note that the rank of a subset of E is the size of the largest partial transversal contained in A. Every transversal matroid is representable over some field, but is binary if and only if it is graphic.
The Fano matroids: The Fano matroid F is the matroid defined on the set E = {1, 2, 3, 4, 5, 6, 7}, whose bases are all those subsets of E with three elements, except {1, 2, 4}, {2, 3, 5}, {3, 4, 6}, {4, 5, 7}, {5, 6, 1}, {6, 7, 2} and {7, 1, 3}.
This matroid can be represented geometrically by Figure. below.
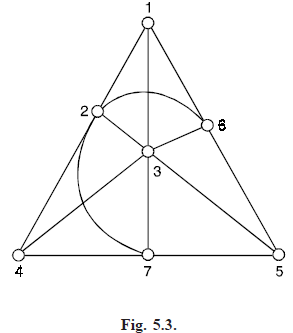
The bases are precisely those sets of three elements that do not lie on a line. It can be shown that F is binary and Eulerian, but is not graphic, cographic, transversal or regular.
Representable matroids: Given a matroid M on a set E, we say that M is representable over a field F if there exist a vector space V over F and a map φ from E to V, such that a subset of A of E is independent in M if and only if φ is one-one on A and φ(A) is linearly independent in V. This amounts to saying that, if we ignore loops and parallel elements, then M is isomorphic to a vector matroid defined in some vector space over F.
For convenience, we say that M is a representable matroid if there exists some field F such that M is representable over F.
Some matroids are representable over every field (the regular matroids), some are representable over no field, and some are representable only over a restricted class of fields. The binary matroids representable over the field of integers modulo 2.
For example. If G is any graph, then its cycle matroids M(G) is a binary matroids. We associate with each edge of G the corresponding row of the incidence matrix of G, regarded as a vector with components 0 or 1. We note that, if a set of edgs of G forms a cycle, then the sum (modulo 2) of the corresponding vectors is 0. A binary matroid that is neither graphic nor cographic is the Fano matroid.
Restrictions and contractions: If M is a matroid defined on set E, and if A is a subset of E, then the restriction of M to A, denoted by M × A, is the matroid whose cycles are precisely those cycles of M that are contained in A. Similarly, the contraction of M to A, denoted by M . A, is the matroid whose cycles are the minimal members of the collection {Ci ∩ A}, where Ci is a cycle of M. A matroid obtained from M by restrictions and/or contractions is called a minor of M.