Vertices
Introduction: A graph is a non-empty finite set V of elements called vertices together with a possibly empty set E of pairs of vertices called edges.
Degree of a Vertices: The number of edges incident on a vertex vi with self-loops counted twice (is called the degree of a vertex vi and is denoted by degG(vi) or deg vi or d(vi). The degrees of vertices in the graph G and H are shown in Figure 4(a) and 4(b).
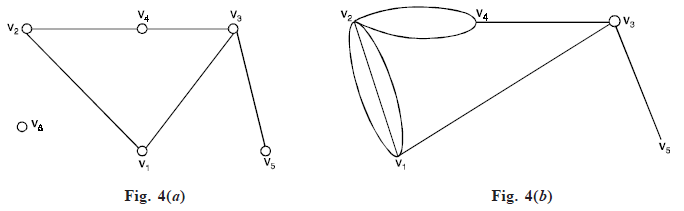
In G as shown in Figure 4(a),
degG (v2) = 2 = degG (v4) = degG (v1), degG (v3) = 3 and degG (v5) = 1 and
In H as shown in Figure 4(b),
degH (v2) = 5, degH (v4) = 3, degH (v3) = 5, degH (v1) = 4 and degH (v5) = 1.
The degree of a vertex is some times also referred to as its valency.
Isolated and Pendent Vertices:
Isolated vertex
A vertex having no incident edge is called an isolated vertex. In other words, isolated vertices are those with zero degree.
Pendent or end vertex
A vertex of degree one, is called a pendent vertex or an end vertex. In the above Figure, v5 is a pendent vertex.
In degree and out degree
In a graph G, the out degree of a vertex vi of G, denoted by out degG (vi) or degG (vi), is the number of edges beginning at vi and the in degree of vi, denoted by in degG (vi) or 1 degG−1 (vi), is the number of edges ending at vi.
The sum of the in degree and out degree of a vertex is called the total degree of the vertex. A vertex with zero in degree is called a source and a vertex with zero out degree is called a sink. Since each edge has an initial vertex and terminal vertex.