Weighted Tree And Prefix Codes

WEIGHTED TREES AND PREFIX CODES: Consider the problem of using bit strings to encode the letters of the English alphabet (where no distinction is made between lower case and upper case letters). We can represent each letter with a bit string of length five, since there are only 26 letters and there are 32 bit strings of length five.

The total number of bits used to encode data is five times the number of characters in the text when each character is encoded with five bits. Is it possible to find a coding scheme of these letters so that, when data are coded, fewer bits are used ? We can save memory and reduce transmittal time if this can be done. Consider using bit strings of different lengths to encode letters. Letters that occur more frequently should be encoded using short bit strings, and longer bit strings should be used to encode rarely occurring letters. When letters are encoded using varying numbers of bits, some method must be used to determine where the bits for each character start and end.

For instance, if e were encoded with 0, a with 1, and t with 01, then the bit string 0101 could correspond to eat, tea, eaea, or tt.

One way to ensure that no bit string corresponds to more than one sequence of letters is to encode letters so that the bit string for a letter never occurs as the first part of the bit string for another letter. Codes with this property are called prefix codes. For instance, the encoding of e as 0, a as 10, and t as 11 is a prefix code.

A word can be recovered from the unique bit string that encodes its letters. For example, the string 10110 is the encoding of ate. To see this, note that the initial 1 does not represent a character, but 10 does represent a (and could not be the first part of the bit string of another letter). Then, the next 1 does not represent a character but 11 does represent t. The final bit, 0, represents e.

A prefix code can be represented using a binary tree, where the characters are the labels of the leaves in the tree. The edges of the tree are labeled so that an edge leading to a left child is assigned a 0 and an edge leading to a right child is assigned a 1. The bit string used to encode a character is the sequence of labels of the edges in the unique path from the root to the leaf that has this character as its label. For instance, the tree in (3.74) represents the encoding of e by 0, a by 10, t by 110, n by 1110, and s by 1111.

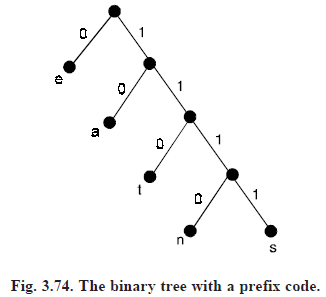
The tree representing a code can be used to decode a bit string. For instance, consider the word encoded by 11111011100 using the code in Fig. (3.74).

This bit string can be decoded by starting at the root, using the sequence of bits to form a path that stops when a leaf is reached. Each 0 bit takes the path down the edge leading to the left child of the last vertex in the path, and each 1 bit corresponds to the right child of this vertex. Consequently, the initial 1111 corresponds to the path starting at the root, going right four times, leading to a leaf in the graph that has s as its label, since the string 1111 is the code for s.

Continuing with the fifth bit, we reach a leaf next after going right then left, when the vertex labeled with a, which is encoded by 10, is visited. Starting with the seventh bit, we reach a leaf next after going right three times and then left, when the vertex labeled with n, which is encoded by 1110, is visited. Finally, the last bit, 0, leads to the leaf that is labeled with e. Therefore, the original word is same.

We can construct a prefix code from any binary tree where the left edge at each internal vertex is labeled by 0 and the right edge by a 1 and where the leaves are labeled by characters. Characters are encoded with the bit string constructed using the labels of the edges in the unique path from the root tothe leaves.