Cauchy’s Mean Value Theorem

Cauchy’s Mean Value Theorem:

If two function f (x) and g (x) are such that:

1. f (x) and g (x) are continuous in the closed intervals [a,b]

2. f (x) and g (x) are differentiable in the open intervals (a,b)

3. g' (x) ≠ 0 for all x ∈ (a,b). Then there exists at least one value c ∈ (a,b) such that

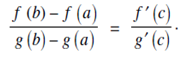
Proof : Let us define a new functions

Where k is constant. From the given condition it is evident that Φ(x) is also continuous in [a,b], differentiable in (a,b). Further we have;

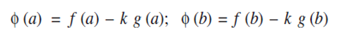
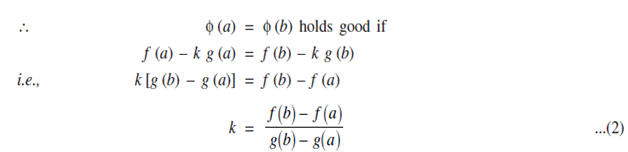
Here g (b) ≠ g (a). Because if g (b) = g (a) then g (x) would satiesfy all the codition Rolle's theroem at least one point c in (a,b) such that g' (c) = 0. This contradicts the data that g' (x) is not equal to zero for all x in (a,b). Hence if k is choosen as given by (2) then Φ(x)satiesfies all the condition of Rolle's theorem.

Differentiate (1) w.r.t x we have;

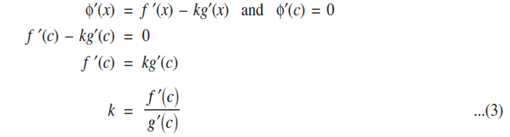
Equating the RHS of (2) and (3) we have;

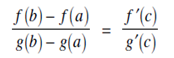
This proves Mean value theroem.