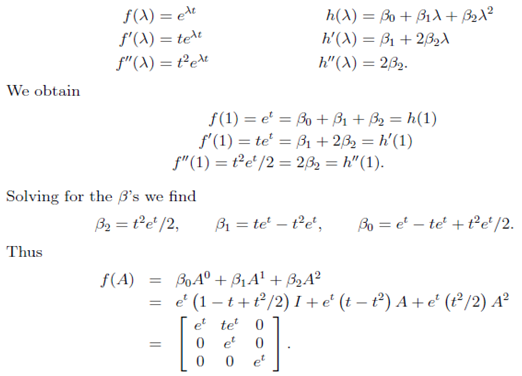Cayley-hamilton Theorem
Cayley-Hamilton Theorem: A linear transformation T from avector space V to itself ( T : V → V ) is called Linear operator on V.
Theorem: Let T : V → Vbe a linear operator on a finite dimensional vector space V. Let p be the charecteristics polynomial of T. Then p (T) = 0.
Proof : Choose a basic β = {v1,.......,vn} for V. I will show that p(T) = 0 by showing that p (T)vi = 0 for all i.
Let A = [T]ββ. Then
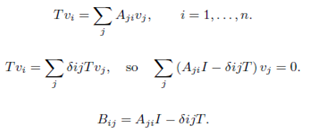
Observe that the matrix B = (B)ij has linear operators as its entries. For example for n = 2.
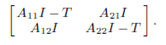
Next i will show that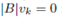 
for all k. Observe that
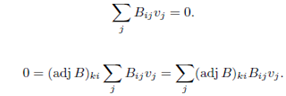
Then the equation hold for all i and k. So interchange the order of summation:
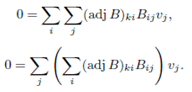
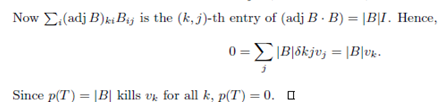
Example- Consider the polynomials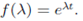 
We obtain three linear equations in three unknown as follows because the eigenvalue of A is repeated twice we must use two derivatives of f and h. Remembering that we are taking derivatives with respect to λ, our equations are
