Diagonalisation Of Matrices

Diagonalisation of Matrices:

Two matrices A,B ∈ M_n(K) are congruent if there is an invertible matrix P ∈ GL_n(K) such that,

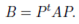
We have shown that if B and C are two bases then for bilinear from f the matrices [ f ]_β and [ f ]_c are congruents.

Theoerem: Let A ∈ Mn(k) be symmetric where k is a field in which 1 1 ≠ 0, then A is congruent to a diagonal matrix.

Proof : This is judt the matrix version of the previous theorem. We shall next find out how to calculate the diagonal matrix congruent to a given symmteric matrix.

Recall : There are three kinds of row operations:

1. Swao rows i and j;

2. Multiply row (i) by λ ≠ 0;

3. Add λ 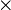$\times \!\,$ row (i) to row (j)

To each row operations there is a corresponding elementery matrix E; then matrix E is the result of doing the row operations to In. The row opeartions transform a matrix A into EA.

We may also define three corresponding column opeartions:

1. Swap column i and j;

2. Multiply column (i) by λ ≠ 0;

3. add λ 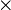$\times \!\,$ column (i) to column (j).

Doing a column operations to A is the same a doing the corresponding row opeartions to A^t. We therefore obtain (EA^t)^t = AE^t .

Example: Consider the quadratic form: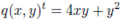

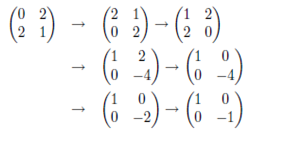
This shows that there is basis {b1,b2} such that,

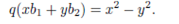
The last step in the previous example transformed the -4 into -1. In general once we have a diagonal matrix we are free to multiply or divide the diagonal entries by square.