Directional Derivative Of Vector

Directional Derivative of Vector:

The derivative of a point function (scalar or vector) in a particular direction is called its directional derivative along the direction. The directional derivative of a scalar point function Φ in a given direction is the rate of change of Φ in the direction. It is given by the component of grad Φ in that direction.

The directional derivatives of a scaler point function Φ (x,y,z) in the direction of . Directional derivatives of Φ is maximum in the direction of Φ. Hence the maximum directional derivatives is .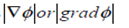

Unit Normal Vector to the Surface:

If Φ (x,y,z) be the scaler function, then Φ (x,y,z) = c represents. A surface and the unit normal vector to the surface Φ is given by .

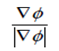
Equation of the tangent plane and normal to the surface:

Suppose 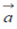is the positive vector of the point (xo,yo,zo). On the surface Φ (x,y,z) = C. If 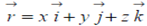position vector of any point (x,y,z) on the tangent plane to the surface Φ at a given point 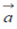on its given by;

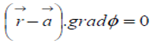
If 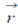is the position vector of any point on the normal to the surface at the point 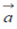on it. The vector equation of the normal at agiven point 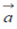on the surface Φ is

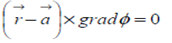
The Cartesian form of the normal at (xo,yo,zo) on the surface of the Φ (x,y,z) = c is;

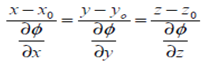
Hence this is the basic Directional Derivative of Vector.