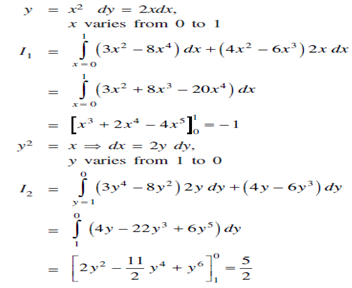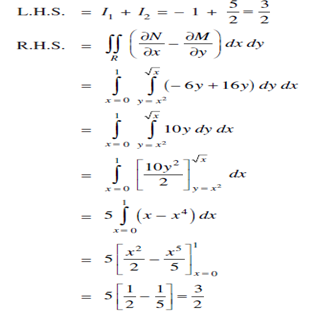Green's Theorem

Green's Theorem: This theorem gives the relation between the plane, surface and the line integrals.

Statement: If R is a closed region in the xy-palne bounded by a simple closed curve C and M (x,y) and N (x,y) are continuous function having the partial derivatives in R then,

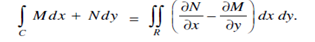
1. Verify Green's Theorem in the plane for 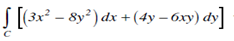where C is the boundary region enclosed by the parabola y² = x and x² = y.

Solution: We shall find the point of intersection of the parabolas

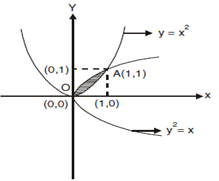
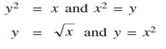
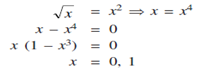
and hence y = 0,1 the point of intersection are (0,0) and (1,1).

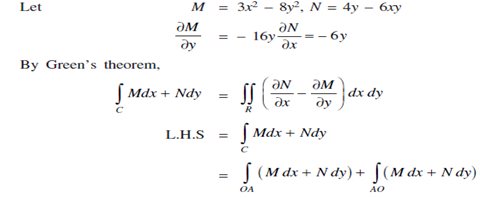
                                                            = I₁ I₂      Along Ao: