Introduction Of Matrices

Introduction of Matrices:

A rectangular array of number is called a matrix. Each number is called the element or entry of the matrix. A Row of a matrix is a horizontal array and a column is a vertical one. The size or order of a matrix is determined by the number of rows and column of that matrix. A matrix is said to be of order or size m 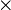$\times \!\,$ n if it has m rows and n column. If m = n, the matrix is called the square matrix of order or size n 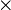$\times \!\,$ n. Any real number is called a scalar.

There are a number of ways to represent an m 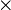$\times \!\,$ n matrix.

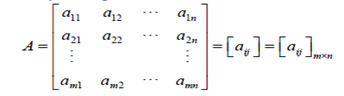
Where a_ij with i = 1,2..... m; j = 1,2....n are called the elements of the matrix.

Example-1:

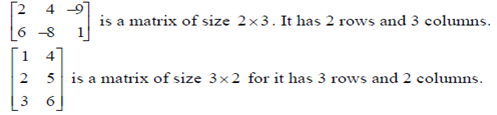
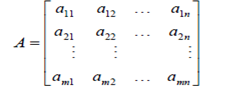
is called a Square matrix of size n 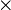$\times \!\,$ n or simply n.

The element a_ijwhere i = j from main diagonal of the matrix. So the matrix

Such amatrix is called a Column Vector as for a 1 $\times \!\,$ n matrix is called a row vector.

Example-2: Consider a matrix;

The diagonal element are denoted by δ; The super diagonal element are denoted by α; and the sub diagonal is denoted by β.