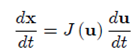Jacobian Of Transformation

Jacobian of Transformation:

In this section, we explore the concept of a "Derivative" of a coordinate transformation, which is known as the Jacobian of the transformation. However, in this course, it is the determinant of the Jacobian that will be used most frequently.

If we let u = < u,v >, p = < p,q >, and x = < x,y >, then (x,y) = T (u,v) is given in vector notation by  X = T (u). This notation allow us to extend the concept of a toatal derivatives to the total derivatives of a coordinate transformation.

Definition: A coordinate transformation T (u) is differentiable at apoint p if there exists a matrix J (p) for which,

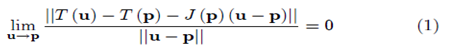
When it exists, J(p) is the total derivatives of T(u) at P. While in non-vector notation the above definition says that total derivatives at apoint (p,q) of a coordinate transformation T (u,v) is a matrix J(u,v) evaluated at (p,q). In manner analogous to that in the above section it can be shown that this matrix is given by

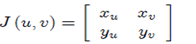
This total derivatives is also known as Jacobians Matrix of the transformation T (u,v).

Example-1: What is the Jacobian Matrix for the polar coordinates transformation.

Solution: 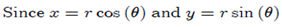the Jacobian Matrix is;

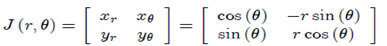
If u (t) = < u (t), v(t) > is the curve in the uv-plane, then x (t) = T ( u (t) , v (t) ) is the image of u (t) in the xy-plane. Hence,

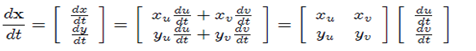
So the last vector is du/dt. Thus we have shown that if X (t) = T (u (t) ), then