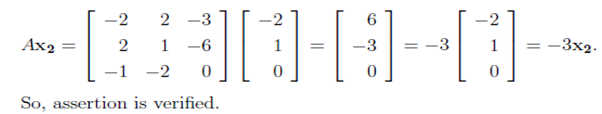Method Of Finding Eigenvalues And Eigenvectors

Method of Finding Eigenvalues and Eigenvectors: Let  A be an n × n matrix:

 

1. To find the eigen value of A solve the characteristics equations

  

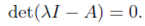
This is a polynomial equation in λ of degree n. We only consider real roots of this equations, in the class.

2. Given an eigenvalue λi to find the eigenspace E(λi) corresponding to λi, we solve the linear system

 

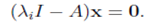
As usual to solve this we reduce it to the row echelon form or Gauss-Jordan form. Since λi is an eigenvalue, at least one row of the echelon form will be zero.

 

Example: Let

 

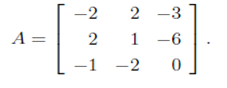
1. Verify that λ₁ = 5 is a eigenvalue of A and X₁ = (1,2,-1)^T is a corresponding eigenvector.

Solution: We need to check AX₁ = 5X₁, we have

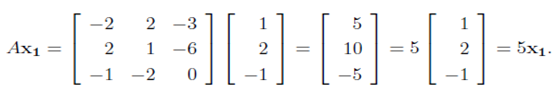
So assertion is verified.

 

2. Verify that λ₂ = - 3 is a eigenvalue of A and x₂ = (-2,1,0)^T is corresponding eigenvector.

Solution: We need to check AX₂ = - 3X₂, we have