Multiple Integrals

Multiple Integrals:

In this topic we discuss a repeated process of integration of a function of two and three variables reffered to as:

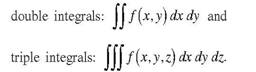
Double Integrals:

The double integral of a function f (x,y) over thw region D in R² is denoted by,

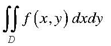
Let f (x,y) be a continuous function in R² defined on a closed rectangle;

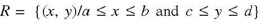
For any fixed x ∈ [a,b] consider the integral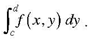

Similarly we can define another;

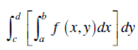
The value of integral depends on the x and we get a new function of x. This can be integrated depends on x and we get;

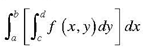This is called Iterated Integrals.

For continuous function f (x,y) we have;

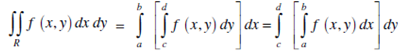
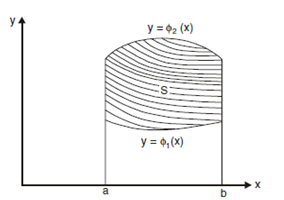
If f (x,y) is continuous on a bounded region S and S is given by,

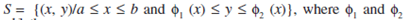are two continuous functions on [a,b] then,

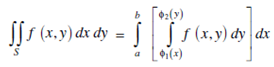
Then, the iterated integral in the R.H.S is also written in the form of

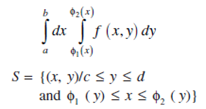
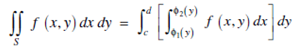
If S can not be written in neither of the above two forms we divide S into finite numbers of subregion such that each of the subregion can be represented in one of the above forms and we get the double integral over S by adding the integrals over these subregion.