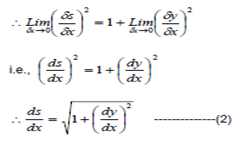Polar Curves
Polar Curves:
If we traverse in a hill section where the road is not straight, we often see caution boards hairpin bend ahead, sharp bend ahead etc. This gives an indication of the difference in the amount of bending of a road at various points which is the curvature at various points. In this chapter we discuss about the curvature, radius of curvature etc.
Consider apoint P in the xy-plane.
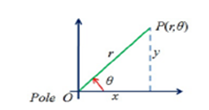
r = length of OP = radial distance
θ = Polar angle
( r, θ ) → Polar co-ordinate
Let r = f (θ) be the polar curves
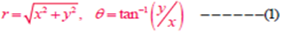
x = r cosθ y = r sinθ
Relation (1) enables us to find the polar co-ordinates ( r, θ ) when the Cartesian coordinates (x,y) are known.
Expression for arc length in Cartesian form:
Proof: Let P (x,y) and Q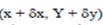 
be two neighboring points on the graph of the functions y = f (x). So that they are at length S and S δs measured from a fixed point A on the curve.
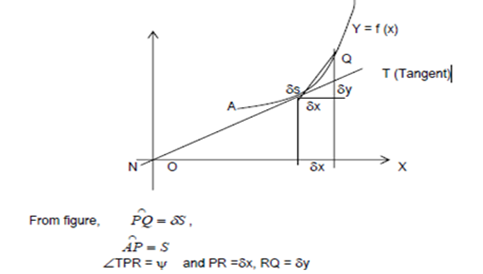
∴ Arc PQ = δS
From Δ PQR, we have
[Chord PQ]2 = PR2 QR2
[Chord PQ]2 = (δx)2 (δy)2
When Q is very close to point P, the length of arc PQ is equal to the length of chord PQ.
i.e Arc PQ = Chord PQ = δs
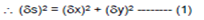
When Q → P along the curve δx → 0, δS → 0.
