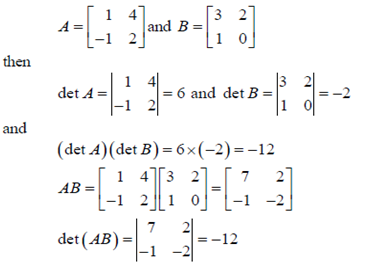←
Maths for Engineers - 1
Properties Of Determinants
Properties of Determinants:
Basic properties of Detaerminants are given as follows:
1. If A is a square matrix then det (A) = det (AT).
Example-1:
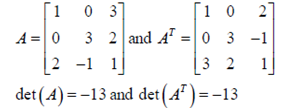
2. A is a square matrix. If we multiply a row or a column of a matrix by a real number u, then determinant of the matrix obtained equals the product of u and determinant of A.
Example-2:
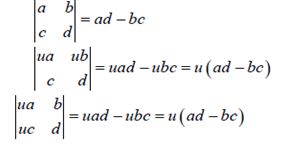
3. If A is a square matrix with two identical row of column, the determinant det (A) = 0.
4. If A is square matrix with a zero row or zero column, then det (A) = 0.
5. If A is a traingular matrix then the determinant of A is the product of main diagonal elements.
6. If A and B are n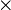 
n, det (AB) = det(A) det (B).
Example-3:
