Rank And Trace Of Matrix

Rank and Trace of  Matrix:

An T×p matrix X is said to be of rank p if the dimension of the largest nonsingular square submatrix is p. (Recall that nonsingular means nonzero determinant, and X is often the matrix of regressors with T observations). The idea of the rank is related to linear independence as follow. We have

        rank(A)= min[ Row rank(A), Column rank(A)],

Where Row rank is the largest number of linearly independent rows, and where Column rank is the largest number of linearly independent columns. In the following example:

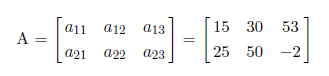
Note that a12 = 2a11 and a22 = 2a21. Hence the first two columns are linearly dependent, and there are only two linearly independent columns. The column rank is only 2. Recall that a set of vectors a1, a2 · · · , and is linearly dependent if a set of scalars ci exists which are not all zero and which satiesfies the expression;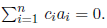

Properties of Rank of Matrix:

Following properties of Rank are useful:

1. rank (X) ≤ min (T,P) which says that the rank of matrix is no greater than the smaller of the two dimension- of rows (T) and column (P). In statistics and econometric text one often encounter the expression that the matrix X of regressor is assumed to be full rank. Since the number of the observation in the regression problems should exceed the number of variables, T > P should hold, which means min (T,P) = p whose rank (X) ≤ p. the rank is the largest it can be and hence we say that X is of full rank.

2. rank (A) = rank (A').

3. rank (A B) ≤ rank (A) rank (B)

4.

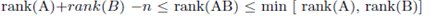
5. If B is non singular rank (AB) = rank (BA) = rank (A)

6. The rank equals the number of non-zero eigen value of a matrix. With the advent of computer programs for eigen value computation. it is some time easier to determine the rank by merely counting the number of non-zero eigenvalue.

Trace of Matrix:

Trace is simply the summation of the diagonal elements. It is also the sum of eigen values.

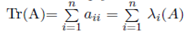
Also note that 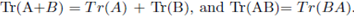It is customery to use the letter result to simplify matrix expression.