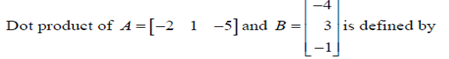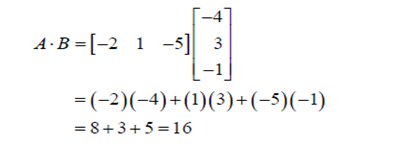Scalar Multiplication

Scalar Multiplication:

Let A = [ a_ij] _m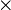nand r be a real number. Then the Scalar Multiplication of the matrix A and the scalar r is a matrix C such that C = [ C_ij] _m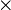nwhere C_ij= r a_ij for all i and j.

Example:

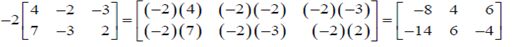
Properties of Scalar Multiplication:

Let r and s be real numbers and A and B be matrices, then

1. r (sA) = (rs) A

2. (r s)A = rA sA

3. r (A B) = rA rB

4. A (rB) = r(AB) = (aA)B

Example:

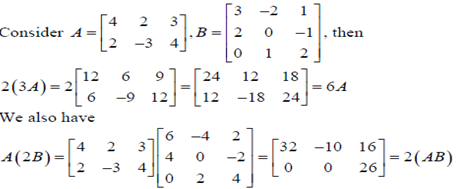
Dot Product:

The Dot Product A.B of a 1 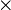$\times \!\,$ n row vector

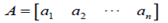
and an n 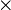$\times \!\,$ 1column vector

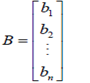
is defined as;

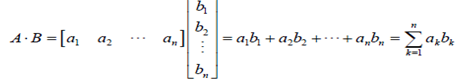
Example:1

Transpose Of Matrix
→
Eigenvalues And Eigenvector
←