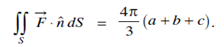Surface And Volume Integrals

Surface and Volume Integrals:

Surface Integral:

An integral evaluated over a surface is called a Surface Integral. Consider a surface S and a point P on it. Let 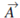be a vector function of x,y,z defined and continuous over S. In 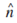is the unit outward normal to the surface S and P then the integral of the normal component of 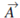at P over the surface S is called the Surface integral written as

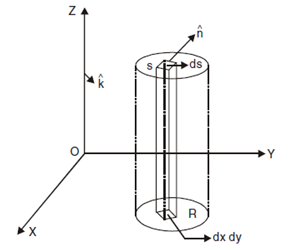
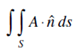
Where ds is the small element area. To evaluate integral we have to find the double integral over the orthogonal projection of the surface on one of the coordinates planes. Suppose R is the orthogonal projection of S on the XOY plane and 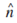.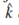ds in the projection of the vectorial element 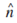ds on the XOY plane and this projection is equal to dx dy which being the area element in the XOY plane. That is to say that 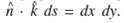Similarly we can argue to state that

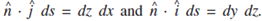All these three results hold good if we write .

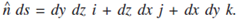Sometimes we also;

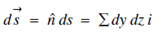
Volume Integral:

If V is the volume bounded by a surface and if F (x,y,z) is asingle valued function defined over V then the volume integral of F (x,y,z) over V is given by

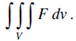If the volume is divided into sub- element having sides dx,dy,dz then the volume integral is given by the triple integral

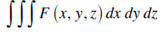which can be evaluated  by choosing appropriate limits for x,y,z.

Example: Evaluate 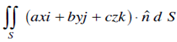Where S is the surface of the sphere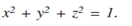

Solution:

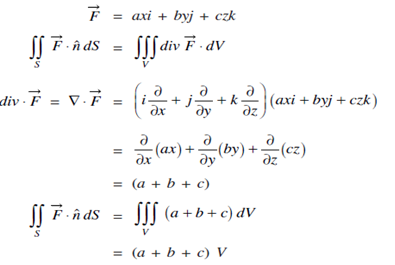
Where V is the volume of the sphere with unit radius and V = 4/3 πr³ for a sphere of radius r.