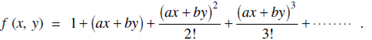Taylor’s Theorem For Function Of Two Variables
Taylor’s Theorem For Function of Two Variables:
Statements: If f (x,y) has continuous partial derivatives up to nth order in a neighbourhood of a point (a,b) then
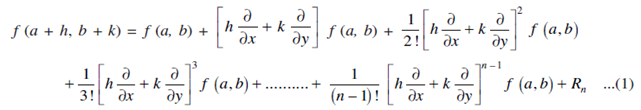
Where,
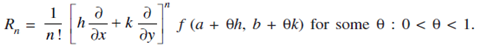
Here Rn is called the remainder after n times. By Taylor's theorem given in
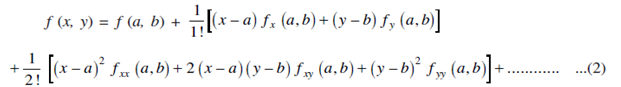
This is called the taylor's theorem of f (x,y) about the point (a,b). If a = 0 and b = 0, we get the Maclaurin's forms of Taylor's Theorem.
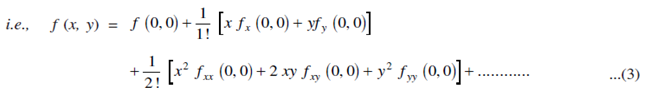
Further if the Taylor's series of f (x,y) is approximated to some terms upto a particular degree the resulting expression of f(x,y) is called as the Taylor's Polynomials.
Example:
Expand e ax by by using Maclaurin's Theorem upto the third term.
Solution: Since the expansion required in power of x, y the point (a,b) associated with (0,0) and the expansion of f (x,y) about (0,0) is given by;
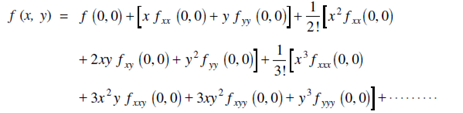
The function and its partial derivatives avaluated at (0,0) is as follows:
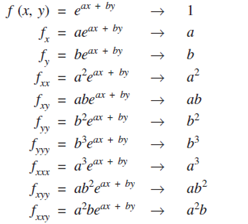
Substitute these value in the expansion of f (x,y), we get;