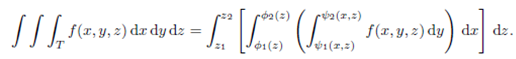Triple Integrals

Triple Integrals:

Properties:

1. Volume Property:

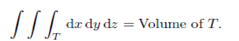
In particular if T is the box T = [a,b] [c,d] [e,f] then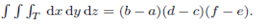

2. Linearity:

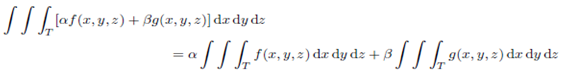
Where α and β are constant.

3. Additivity:

If T is broken up into a finite number of non overlapping basic region T1, T2,...........Tn, then

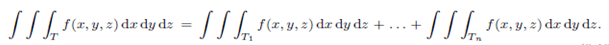
Evaluation of Triple Integral by Repeated Integrals:

Let T be a solid whose projection onto the xy-plane is labelled Ωxy. Then the solid T is set of all points (x,y,z) satisfying

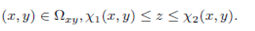
The tripple integral over T can be evaluated by setting

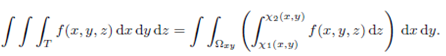
Now the triple integral over T can be expressed by three ordinary integrals as:

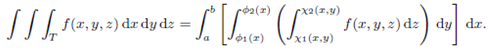
There is nothing special about this order of integration. Otherwise order of integration are possible and in some cases more convienient. Suppose for example that the projection of T onto the xz-plane is domain Ωxz of the form

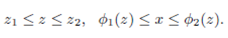
If T is set of all (x,y,z) with

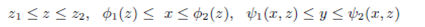
Then