Unitary Matrices

Unitary Matrices:

A n 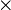n matrix A and B are unitarily similar if there exists a unitary matrix U such that U*AU = B.

Theorem: (Schur's Theorem) Every square matrix is unitary similar to an upper traingular matrix (in Cⁿ).

Proof : We use induction. case n = 1 is trival. We assume that the claims hold for (n-1)X(n-1) matrices. Let A be an nxn matrix, λ₁ its eigenvalue and x₁ correspoding normalized eigenvector 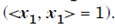We construct an orthogonal basis for Cⁿ incuding x₁ as the first vector. The bais is of form of:

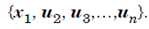
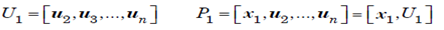
the matrix P1 is unitary and

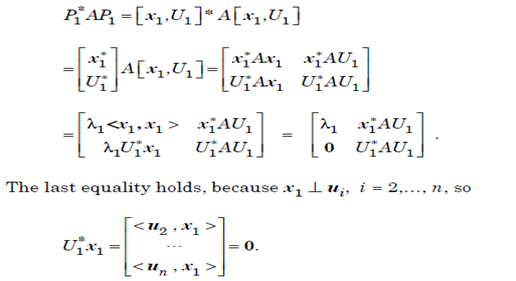
U1* AU1 ia an (n-1)x(n-1) matrix so the induction hypothesis that there exists a unitary matrix Q2 such that,

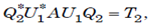
Direct computation shows us that P2 is unitary and

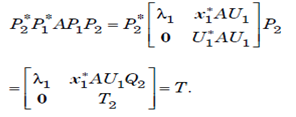
The product P1 and P2 of two unitary matrices is unitary and T is an upper traingular matrix, so we have proven the claim.