Vector Functions

Vector Functions:

A Vector - Valued function 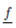is a vector function whose components are single - valued functions (Scaler Valued Function). For example, given three single valued function f₁(t) , f₂(t), f₃(t) we can form the vector valued functions:

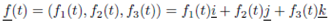
The magnitude of the vector valued function 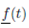is scaler valued function and is defined by

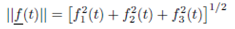
In general the graph of the vector function 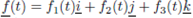is acurve C, in the sense that, as t varies thetip of the position vector 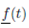trances out C. The equation

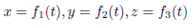
Corresponding to the component of 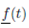are the parametric equations of C.

Derivative of a Vector Function:

Given the vector function 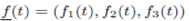the derivatives of 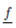is defined by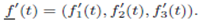

Properties of the Derivatives:

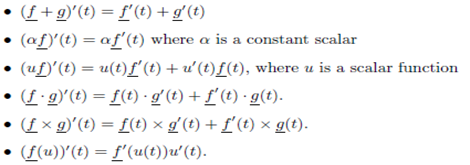
Integral of Vector Functions:

Given the vector function 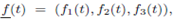the integral of 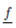is defined by

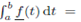
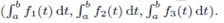
Properties of the Integrals:

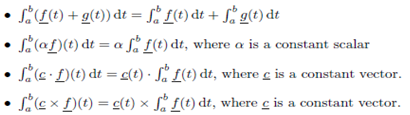
Curves:

1. The equation of a straight line is parametrised by

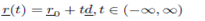
2. More generally, every vector function

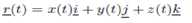
Parametrise a Curve in Space.