Bessel Equation
Bessel Equation:
The second order differential equation given as:
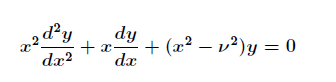
is known as Bessel’s Equation. Where the solution to Bessel’s equation yields Bessel functions of the first and second kind as follows:
![]()
where A and B are arbitrary constants. While Bessel functions are often presented in text books and tables in the form of integer order, i.e. ν = 0, 1, 2, . . . , in fact they are defined for all real values of −∞ < ν < ∞.
Bessel Functions: Bessel’s differential equation, given as:
![]()
is often encountered when solving boundary value problems, such as separable solutions to Laplace’s equation or the Helmholtz equation, especially when working in cylindrical or spherical coordinates. The constant ν, determines the order of the Bessel functions found in the solution to Bessel’s differential equation and can take on any real numbered value. For cylindrical problems the order of the Bessel function is an integer value (ν = n) while for spherical problems the order is of half integer value (ν = n 1/2). Since Bessel’s differential equation is a second-order equation, there must be two linearly independent solutions. Typically the general solution is given as: where the special functions Jν(x) and Yν(x) are:
1. Bessel functions of the first kind, Jν(x), which are finite at x = 0 for all real values of v.
2. Bessel functions of the second kind, Yν(x), (also known as Weber or Neumann functions) which are singular at x = 0
The Bessel function of the first kind of order ν can be be determined using an infinite power series expansion as follows:
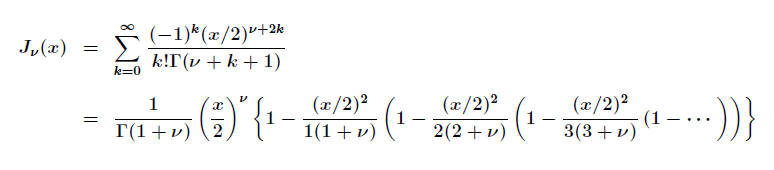
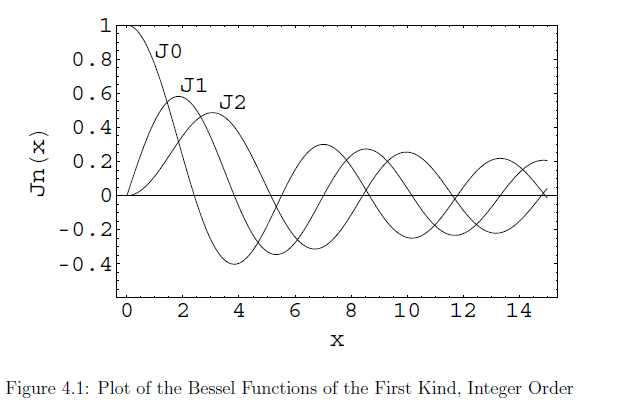
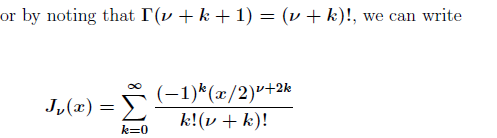
Bassel's Function of First Kind of order 0,1,2 are shown in the above figure.