Heisenberg's Inequaity
Heisenberg's Inequality:
This is the Basic Heiseberg's Inequality Theorem:
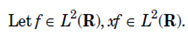
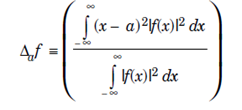
is called the Dispersion about the point x = a of f. The reasioning behind the definition is that if f (x) is concentrated near x = a, then Δa f is smaller than when f is not close to zero far from x = a.
Example: Consider the charectristic functions:
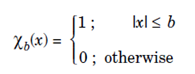
Which has Fourier Transform
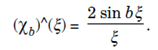
Notice that xb is concentrated near x = 0 for small b. The dispersion about the origin is
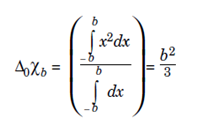
and it clear that the dispersion increases as b increases. Notice that the Fourier transform xb^ does not have a finite dispersion about the origin.
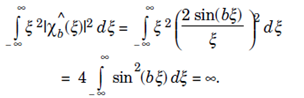
The Following results shows that there is a type of inverse relationship between the dispersion of a function and that of its Fourier Transform.